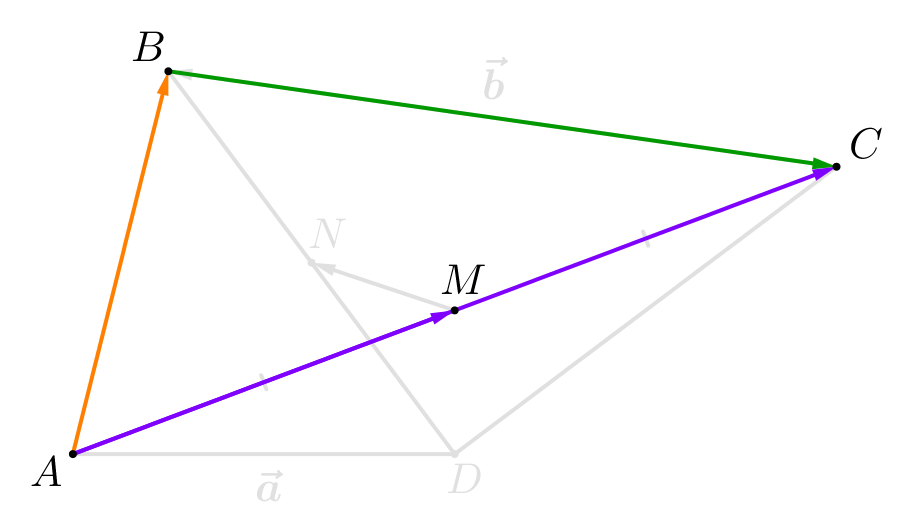
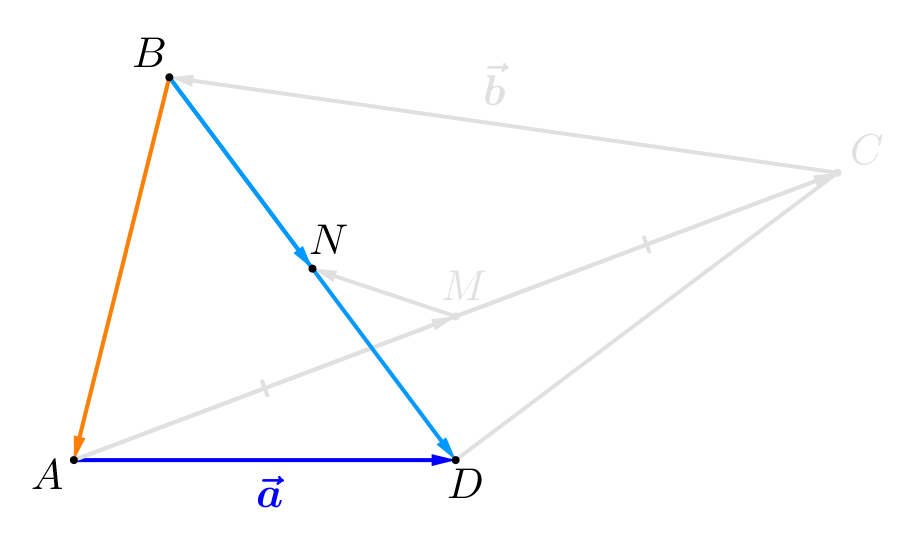
В четырехугольнике \(\displaystyle ABCD\) точка \(\displaystyle M\) – середина диагонали \(\displaystyle AC\small,\) а \(\displaystyle N\) – середина диагонали \(\displaystyle BD\small.\)
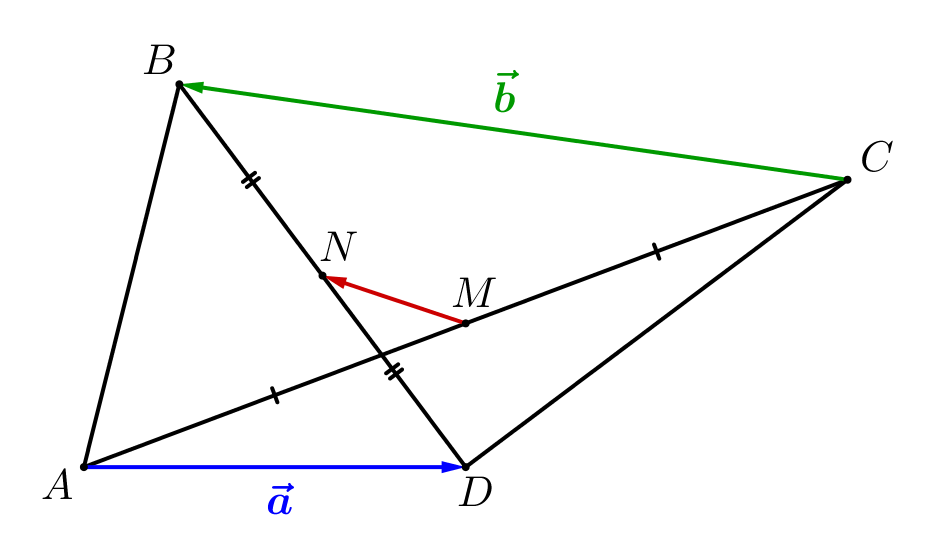
Обозначим векторы \(\displaystyle \overrightarrow{AD}=\vec{a}\) и \(\displaystyle \overrightarrow{CB}=\vec{b}\small.\) Выразите вектор \(\displaystyle \overrightarrow{MN}\) через \(\displaystyle \vec{a}\) и \(\displaystyle \vec{b}\small.\)
Будем выражать вектор \(\displaystyle MN\) через векторы, соответствующие сторонам четырехугольника.
По правилу многоугольника: \(\displaystyle \overrightarrow{MN}=\overrightarrow{MC}+\overrightarrow{CB}+\overrightarrow{BN}=\overrightarrow{MC}+\vec{b}+\overrightarrow{BN}\small.\) | 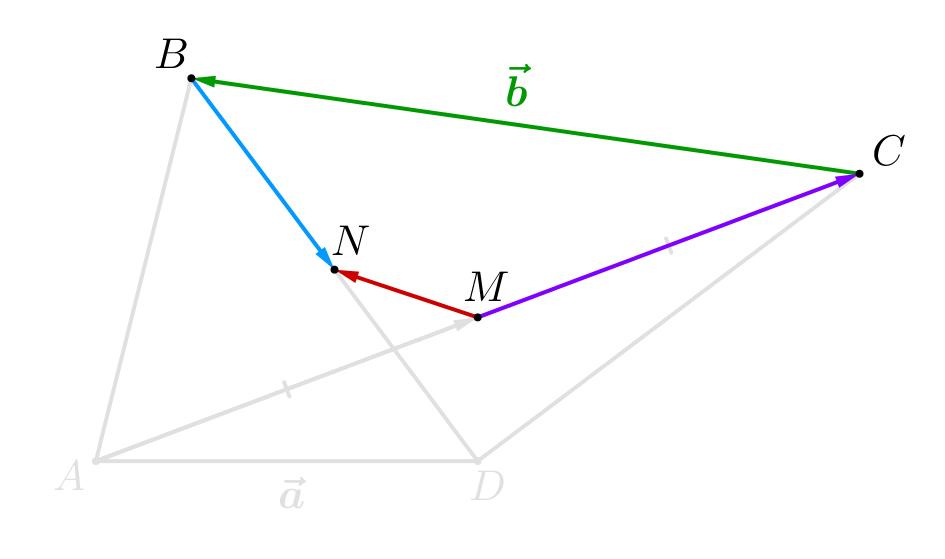 |
Теперь выразим \(\displaystyle \overrightarrow{MC}\) и \(\displaystyle \overrightarrow{BN}\) через векторы, соответствующие сторонам четырехугольника.
Помимо векторов \(\displaystyle \vec{a}\) и \(\displaystyle \vec{b}\) будем использовать вектор \(\displaystyle \overrightarrow{AB}{\small:}\)
\(\displaystyle \overrightarrow{MC}=\frac{1}{2}\left(\overrightarrow{AB}+\overrightarrow{BC}\right)=\frac{1}{2}\left(\overrightarrow{AB}-\vec{b}\right)\small.\)
\(\displaystyle \overrightarrow{BN}=\frac{1}{2}\left(\overrightarrow{BA}+\overrightarrow{AD}\right)=\frac{1}{2}\left(-\overrightarrow{AB}+\vec{a}\right)\small.\)
Подставляя, получаем:
\(\displaystyle \overrightarrow{MN}=\overrightarrow{MC}+\vec{b}+\overrightarrow{BN}=\frac{1}{2}\left(\overrightarrow{AB}-\vec{b}\right)+\vec{b}+\frac{1}{2}\left(-\overrightarrow{AB}+\vec{a}\right)=\frac{1}{2}\vec{a}+\frac{1}{2}\vec{b}\small.\)
Ответ: \(\displaystyle \overrightarrow{MN}=\frac{1}{2}\vec{a}+\frac{1}{2}\vec{b}\small.\)