Стороны \(\displaystyle AB\) и \(\displaystyle BC\) параллелограмма равны \(\displaystyle 3\) и \(\displaystyle 4\small.\) Найдите площадь этого параллелограмма, если \(\displaystyle \left|2\cdot\overrightarrow{AB}+\overrightarrow{BD}\right|=5\small.\)
Попробуем воспользоваться условием \(\displaystyle \left|2\cdot\overrightarrow{AB}+\overrightarrow{BD}\right|=5\small.\)
Продлим отрезок \(\displaystyle AB\) за точку \(\displaystyle B\) на расстояние \(\displaystyle \left|\overrightarrow{AB}\right|\small.\) Получили вектор \(\displaystyle \overrightarrow{AN}=2\overrightarrow{AB}\small.\) Отрезок \(\displaystyle BN\) равен и параллелен отрезку \(\displaystyle CD\small.\) Тогда \(\displaystyle BNCD\) – параллелограмм. Значит, \(\displaystyle \overrightarrow{NC}=\overrightarrow{BD}\small.\) Получаем: \(\displaystyle 2\cdot\overrightarrow{AB}+\overrightarrow{BD}=\overrightarrow{AN}+\overrightarrow{NC}=\overrightarrow{AC}\small.\) | 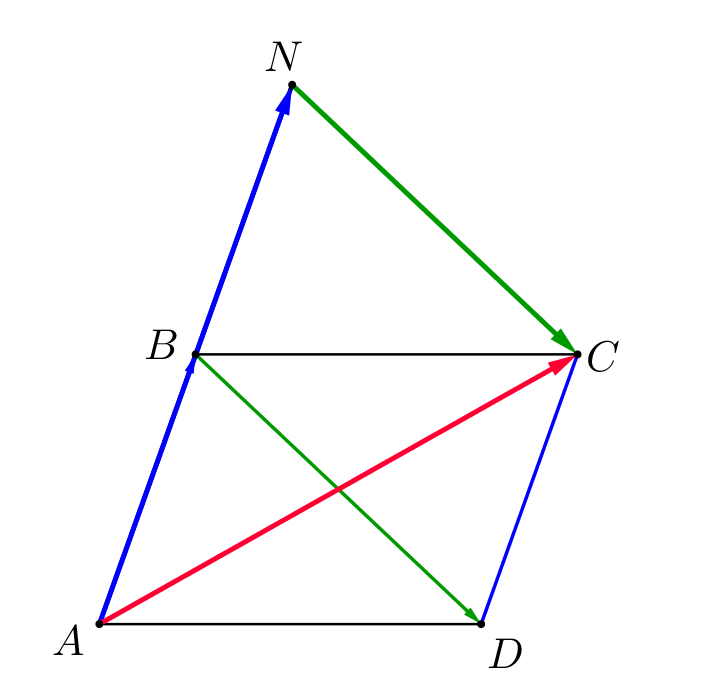 |
То есть
\(\displaystyle \left|\overrightarrow{AC}\right|=\left|2\cdot\overrightarrow{AB}+\overrightarrow{BD}\right|=5\small.\)
Получаем, что стороны параллелограмма \(\displaystyle AB=3,\,BC=4\) и диагональ \(\displaystyle AC=5\small.\)
Противоположные стороны параллелограмма равны. Тогда стороны треугольника \(\displaystyle ACD\) равны \(\displaystyle 3,\,4,\,5\small.\)
\(\displaystyle \angle ADC=90^{\circ}\small.\)
В параллелограмме один из углов прямой. Значит, это прямоугольник. А площадь прямоугольника равна произведению соседних сторон: \(\displaystyle S_{ABCD}=AB\cdot AD=3\cdot4=12\small.\) | 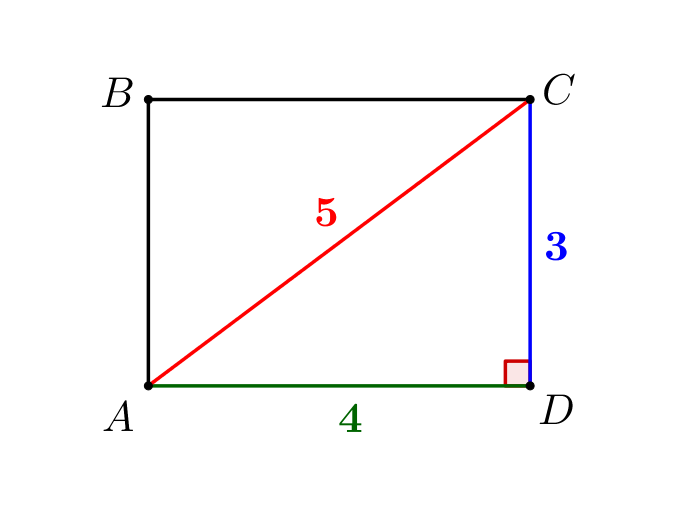 |
Ответ: \(\displaystyle S_{ABCD}=12\small.\)