Задание
На рисунке отмечены точки \(\displaystyle A,\,B\) и \(\displaystyle M\small.\)
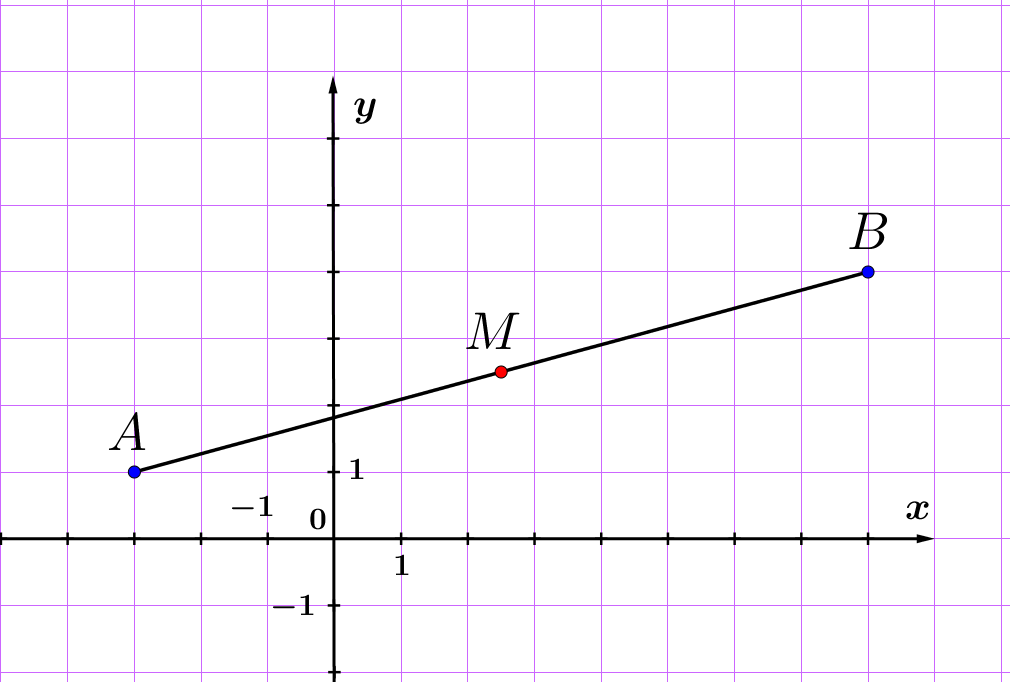
Найдите координаты точки \(\displaystyle M\small,\) если \(\displaystyle M\) середина отрезка \(\displaystyle AB\small.\)
\(\displaystyle x_m=\) и \(\displaystyle y_m=\)
Решение
Правило
Координаты середина отрезка
Координаты середины отрезка равны полусумме координат концов.
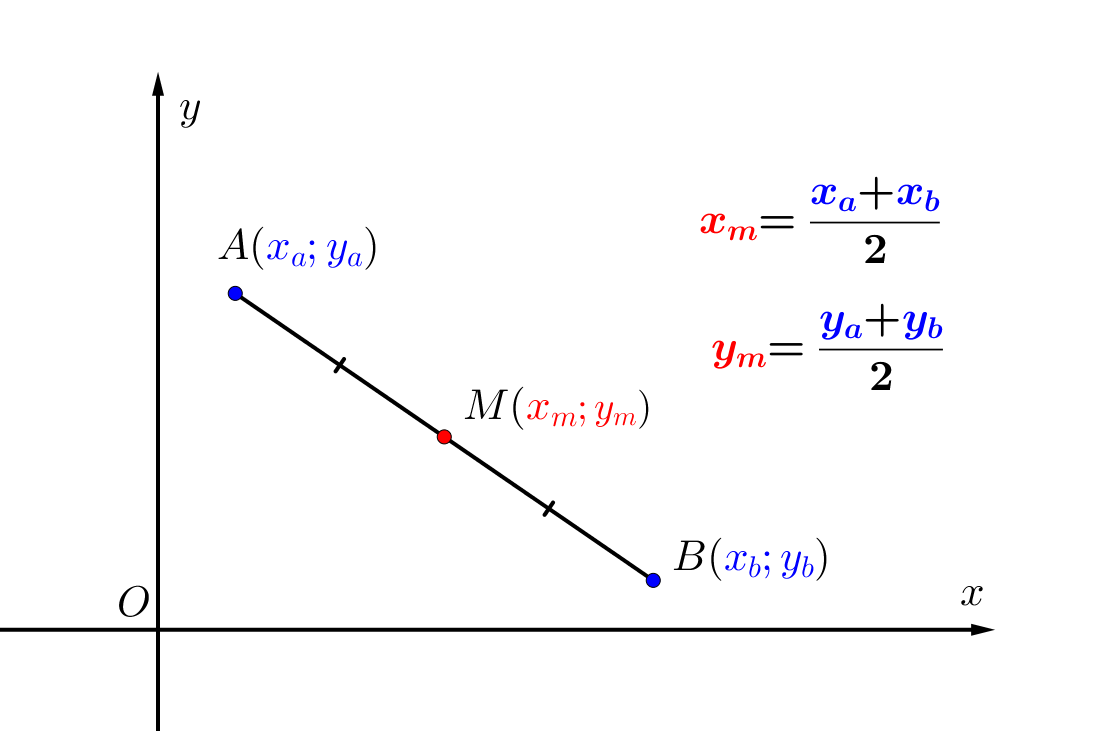
Из рисунка видим, что координаты точек \(\displaystyle A(-3;1)\) и \(\displaystyle B(8;4)\small.\)
Тогда координаты точки \(\displaystyle M{\small:}\)
\(\displaystyle x_m=\frac{-3+8}{2}=\frac{5}{2}=2{,}5\small,\)
\(\displaystyle y_m=\frac{1+4}{2}=\frac{5}{2}=2{,}5\small.\)
Ответ: \(\displaystyle M(2{,}5;2{,}5).\)