Задание
Найдите медиану \(\displaystyle AM\) треугольника \(\displaystyle ABC\small,\) координаты вершин которого равны: \(\displaystyle A(1;\,1),\,B(3;\,4),\,C(-1;-4)\small.\)
\(\displaystyle AM=\)
Решение
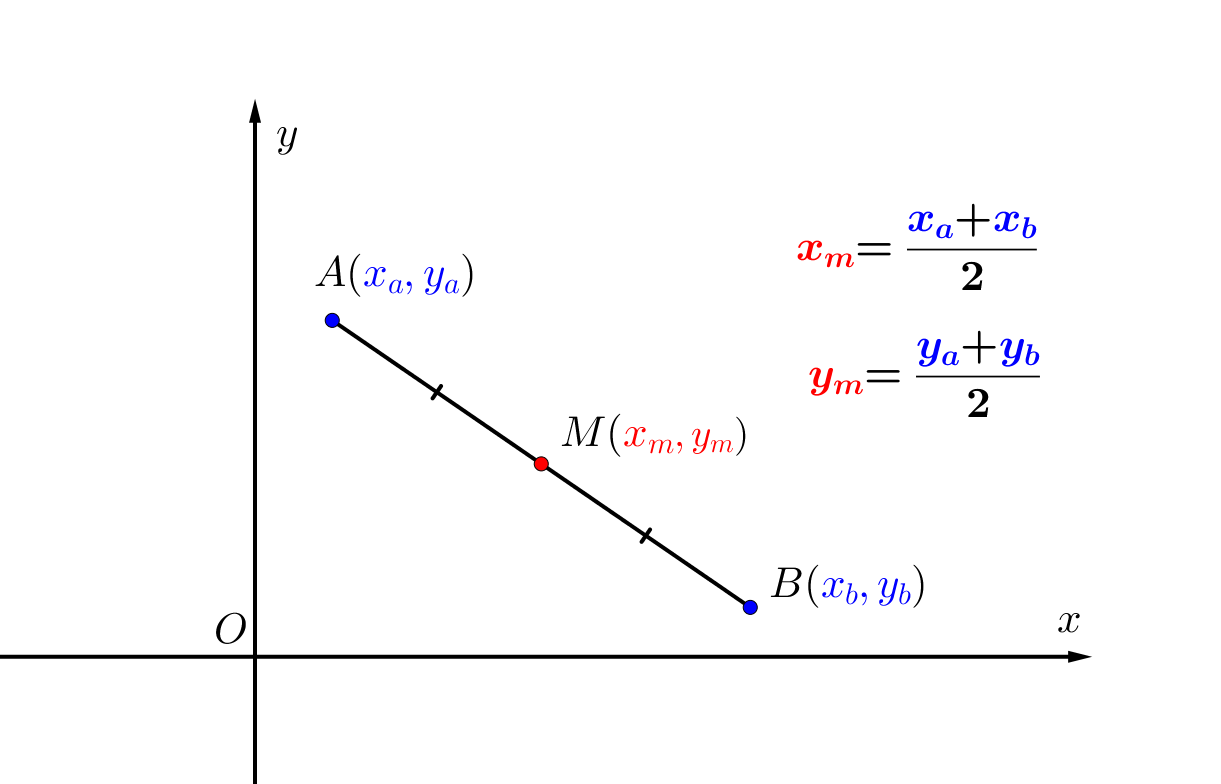
Точка \(\displaystyle M~-\) середина стороны \(\displaystyle BC\small.\) Тогда координаты \(\displaystyle M{\small:}\) \(\displaystyle M\left(\frac{3+(-1)}{2};\,\frac{4+(-4)}{2}\right)=M(1;0)\small.\) Расстояние между точками \(\displaystyle A(1;\,1)\) и \(\displaystyle M(1;0)\) равно \(\displaystyle 1\small.\) | 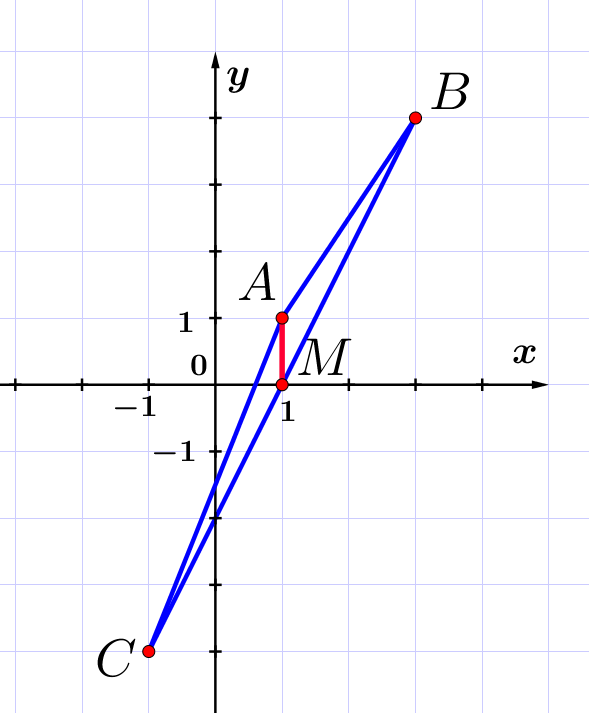 |
Ответ: \(\displaystyle AM=1\small.\)