Заполните таблицу, если \(\displaystyle M~-\)середина отрезка \(\displaystyle AB\small.\)
| Координаты \(\displaystyle A\) | \(\displaystyle (3;\,4)\) | \(\displaystyle \big(\) | \(\displaystyle (2t+3;\,5-4t)\) |
| Координаты \(\displaystyle B\) | \(\displaystyle (-2;\,7)\) | \(\displaystyle (3;\,4)\) | \(\displaystyle \big(\) |
| Координаты \(\displaystyle M\) | \(\displaystyle \big(\) | \(\displaystyle (-1;\,7)\) | \(\displaystyle (t+2;\,3-2t)\) |
Воспользуемся правилом:
Координаты середина отрезка
Координаты середины отрезка равны полусумме координат концов.
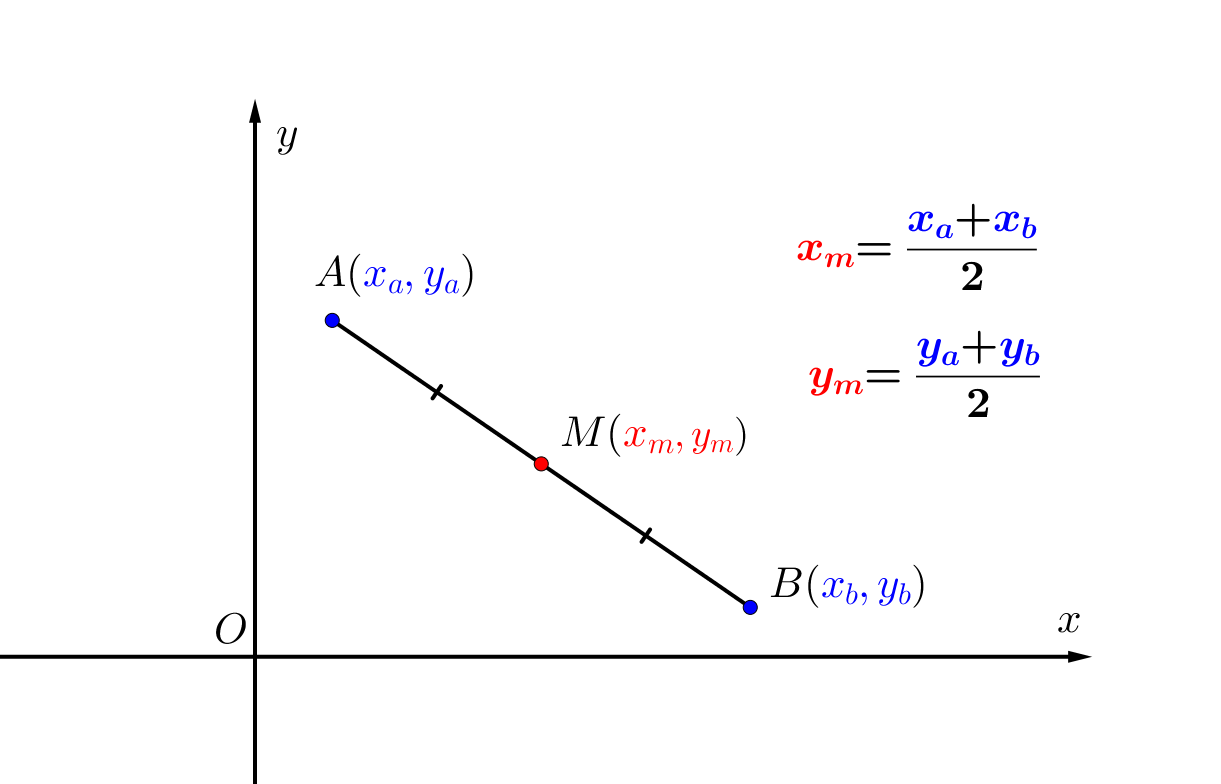
Отдельно рассмотрим каждый из столбцов.
Координаты концов отрезка: \(\displaystyle A(3;\,4)\) и \(\displaystyle B(-2;\,7)\small.\) Тогда координаты середины отрезка: \(\displaystyle M\left(\frac{3+(-2)}{2};\,\frac{4+7}{2}\right)=M\left(\frac{1}{2};\,\frac{11}{2}\right)\small.\)
Известны координаты одного из концов отрезка \(\displaystyle B(3;\,4)\) и координаты середины отрезка \(\displaystyle M(-1;\,7)\small.\) Обозначим координаты второго конца \(\displaystyle A(x;\,y)\small.\) Тогда \(\displaystyle -1=\frac{3+x}{2}\) и \(\displaystyle 7=\frac{4+y}{2}\small.\) Решая уравнения, находим \(\displaystyle x\) и \(\displaystyle y{\small:}\) \(\displaystyle x=-5\) и \(\displaystyle y=10\small.\) То есть координаты точки \(\displaystyle A(-5;\,10)\small.\)
Известны координаты одного из концов отрезка \(\displaystyle A(2t+3;\,5-4t)\) и координаты середины отрезка \(\displaystyle M(t+2;\,3-2t)\small.\) Обозначим координаты второго конца \(\displaystyle B(x;\,y)\small.\) Тогда \(\displaystyle t+2=\frac{2t+3+x}{2}\) и \(\displaystyle 3-2t=\frac{5-4t+y}{2}\small.\) Решая уравнения, находим \(\displaystyle x\) и \(\displaystyle y{\small:}\) \(\displaystyle 2(t+2)=2t+3+x\) и \(\displaystyle 2(3-2t)=5-4t+y\small.\) \(\displaystyle x=1\) и \(\displaystyle y=1\small.\) То есть координаты точки \(\displaystyle B(1;\,1)\small.\)
Заполняя таблицу, получаем:
| Координаты \(\displaystyle A\) | \(\displaystyle (3;\,4)\) | \(\displaystyle (-5;\,10)\) | \(\displaystyle (2t+3;\,5-4t)\) |
| Координаты \(\displaystyle B\) | \(\displaystyle (-2;\,7)\) | \(\displaystyle (3;\,4)\) | \(\displaystyle (1;\,1)\) |
| Координаты \(\displaystyle M\) | \(\displaystyle \left(\frac{1}{2};\,\frac{11}{2}\right)\) | \(\displaystyle (-1;\,7)\) | \(\displaystyle (t+2;\,3-2t)\) |