Изображённую на клетчатой бумаге фигуру разрезали на четыре равных фигуры по линиям разметки.
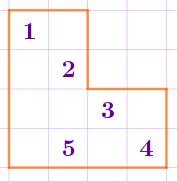
Какие две цифры оказались в одной из четырёх получившихся фигур?
В ответе запишите две цифры в порядке возрастания без разделителей \(\displaystyle -\) как двузначное число.
Найдём нужную разметку. Для этого определим форму равных частей, на которые разрезается фигура.
Всего в исходной фигуре \(\displaystyle 12\) клеток. Значит, каждая из равных частей должна состоять из трёх клеток:
\(\displaystyle \frac{12}{4}=3{\small .}\)
Из трёх клеток можно сложить только две фигуры. Две клетки должны примыкать друг к другу. Третья примыкает:
- к короткой стороне образующегося прямоугольника, и получается "палочка";
- или к длинной стороне, и получается "уголок".
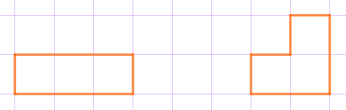
Попробуем закрыть "палочкой" клетку, которую отметим буквой \(\displaystyle a{\small .}\)
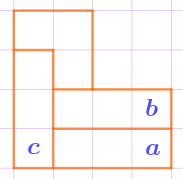
Это можно сделать, только уложив палочку горизонтально. Аналогичная ситуация с размещением кусочка, закрывающего клетку \(\displaystyle b{\small .}\)
Для клетки \(\displaystyle c\) теперь также остаётся только один вариант.
Кусочек, оставшийся после размещения трёх "палочек", четвёртой уже не покрывается.
Удобно начать разрезание с той же клетки \(\displaystyle a{\small .}\)
Получается только три способа размещения первых двух, примыкающих друг к другу "уголков".
Два из них быстро заводят нас в тупик, а в результате третьего получается следующая разметка.
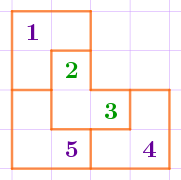
Видим, что в границы одной части попадают метки \(\displaystyle 2\) и \(\displaystyle 3{\small .}\) Записываем их в ответ в порядке возрастания.
Ответ: \(\displaystyle 23{\small .}\)