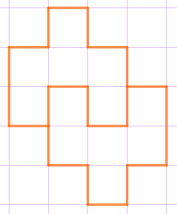
Изображённую на клетчатой бумаге фигуру разрезали на две равные части.
Из этих частей составили другую фигуру. Найдите её среди предложенных вариантов.
| ИСХОДНАЯ ФИГУРА | НОВАЯ ФИГУРА |
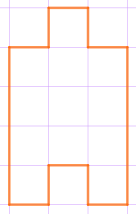 |
В исходной фигуре \(\displaystyle 12\) клеток.
Значит, для каждой из двух её равных частей количество клеток равно шести:
\(\displaystyle \frac{12}{2}=6{\small .}\)
Отметим три клетки исходной фигуры буквами \(\displaystyle a{\small ,\;}b\) и \(\displaystyle c{\small .}\)
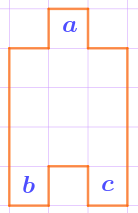
Клетка \(\displaystyle a\) не может попасть в одну из равных частей ни с клеткой \(\displaystyle b{\small ,}\) ни с клеткой \(\displaystyle c{\small .}\) Иначе такая часть измерялась бы пятью клетками по вертикали.
Но вторая часть той же протяжённости на рисунок уже не укладывается. Не хватает клеток ни по вертикали, ни по горизонтали.
Значит, в одной части расположена клетка \(\displaystyle a\small,\) а в другой \(\displaystyle -\) клетки \(\displaystyle b\) и \(\displaystyle c{\small .}\)
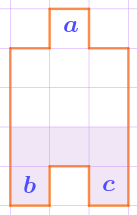
Чтобы соединить эти две клетки одной части, требуется ещё три клетки. Остаётся только рассмотреть три варианта для расположения шестой клетки. Подходит только один из них:
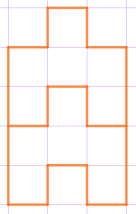
Только одна из получающихся при этом фигур совпадает с одним из предложенных вариантов ответа:
| Ответ: | 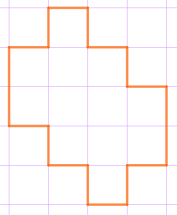 |