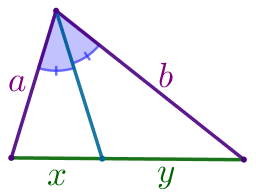
Биссектриса угла равнобедренного треугольника делит его боковую сторону на отрезки с длинами \(\displaystyle 3\) и \(\displaystyle 8{\small,}\) считая от основания. Найдите периметр этого треугольника.
По условию задачи выполним построение.
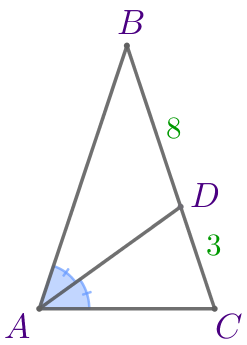 | Пусть \(\displaystyle ABC\) – треугольник:
Требуется найти периметр треугольника. |
Периметр треугольника равен сумме длин всех его сторон:
\(\displaystyle P_{\triangle ABC}=AB+BC+AC{\small.}\)
Найдём стороны треугольника.
\(\displaystyle AB=BC=11{\small.}\)
\(\displaystyle \frac{AB}{AC}=\frac{BD}{DC}{\small.}\)
Значит, \(\displaystyle \frac{AB}{AC}=\frac{8}{3}{\small.}\) То есть \(\displaystyle AB=8t{\small,}\) \(\displaystyle AC=3t{\small.}\) | 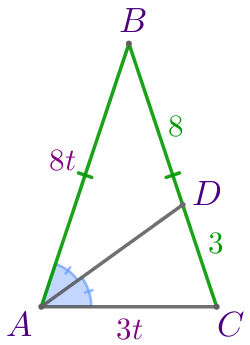 |
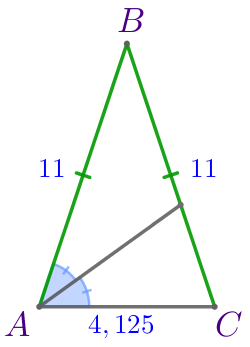 | Так как \(\displaystyle AB=11{\small,}\) то \(\displaystyle 8t=11{\small;}\) \(\displaystyle t=\frac{11}{8}{\small.}\) Тогда \(\displaystyle AC=3t=3 \cdot \frac{11}{8}=\frac{33}{8}=4{,}125{\small.}\) |
В результате получаем:
\(\displaystyle P_{\triangle ABC}=AB+BC+AC=11+11+4{,}125=26{,}125{\small.}\)
Ответ: \(\displaystyle 26{,}125{\small.}\)