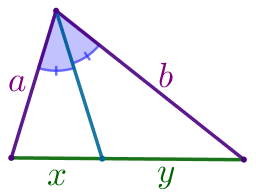
Одна из биссектрис треугольника делится точкой пересечения биссектрис в отношении \(\displaystyle 47:14{\small,}\) считая от вершины. Найдите периметр треугольника, если длина стороны треугольника, к которой эта биссектриса проведена, равна \(\displaystyle 28{\small.}\)
По условию задачи выполним построение.
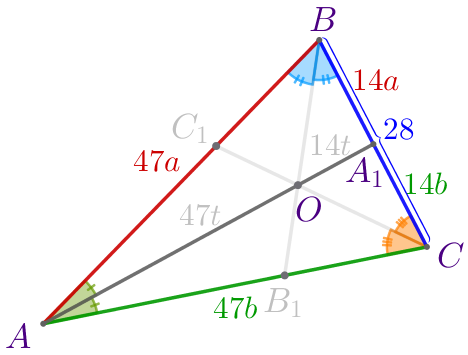
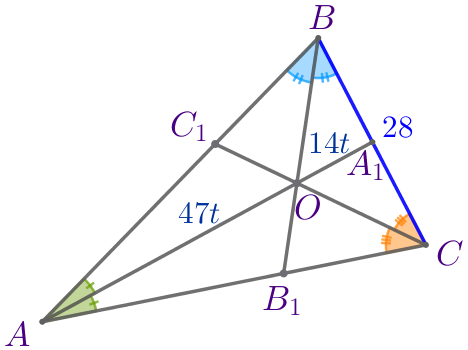 | Пусть \(\displaystyle ABC\) – треугольник:
\(\displaystyle AO=47t{\small,}\) \(\displaystyle OA_1=14t{\small.}\) Требуется найти периметр треугольника. |
Периметр треугольника равен сумме длин всех его сторон:
\(\displaystyle P_{\triangle ABC}=AB+AC+BC{\small.}\)
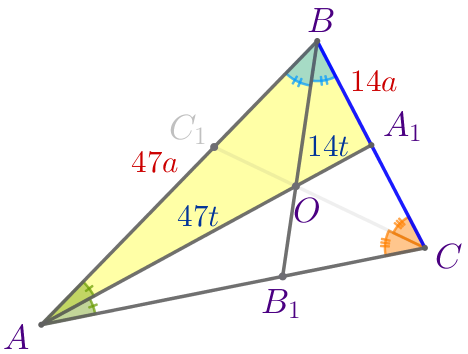
| \(\displaystyle BO\) – биссектриса. По свойству биссектрисы треугольника: \(\displaystyle \frac{AB}{BA_1}=\frac{AO}{OA_1}=\frac{47}{14}{\small.}\) Значит, \(\displaystyle AB=47a{\small,}\) \(\displaystyle BA_1=14a{\small.}\) |
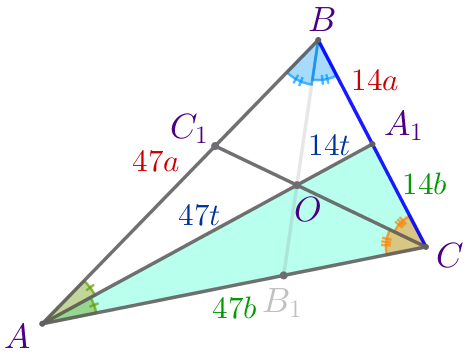
| \(\displaystyle CO\) – биссектриса. По свойству биссектрисы треугольника: \(\displaystyle \frac{AC}{CA_1}=\frac{AO}{OA_1}=\frac{47}{14}{\small.}\) Значит, \(\displaystyle AC=47b{\small,}\) \(\displaystyle CA_1=14b{\small.}\) |
 |
\(\displaystyle BC=14a+14b=14 \cdot (a+b){\small.}\) По условию \(\displaystyle BC=28{\small,}\) значит, \(\displaystyle 14 \cdot (a+b)=28{\small;}\) \(\displaystyle (a+b)=2{\small.}\) |
В результате получаем:
\(\displaystyle\begin{aligned}P_{\triangle ABC}&=AB+AC+BC=\\&=47a+47b+28=47 \cdot (a+b)+28{\small.}\end{aligned}\)
Подставим \(\displaystyle (a+b)=2{\small:}\)
\(\displaystyle P_{\triangle ABC}=47 \cdot 2 +28=94+28=122{\small.}\)
Ответ: \(\displaystyle 122{\small.}\)