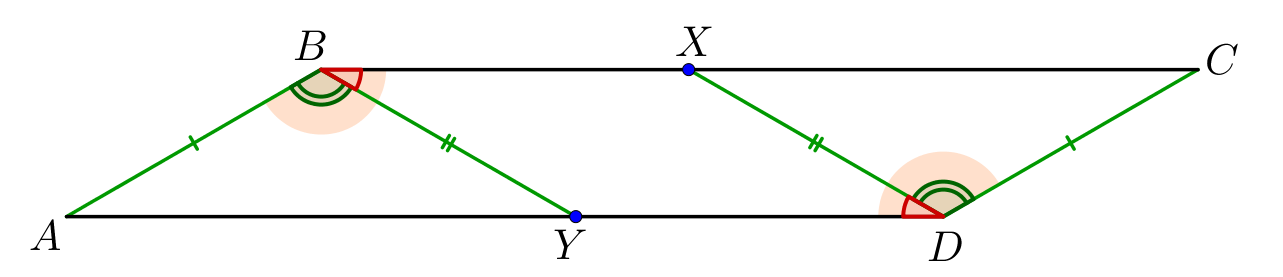
В параллелограмме \(\displaystyle ABCD\) на сторонах \(\displaystyle BC\) и \(\displaystyle AD\) выбрали точки \(\displaystyle X\) и \(\displaystyle Y\small.\) При этом оказалось, что прямые \(\displaystyle BY\) и \(\displaystyle DX\) параллельны. Найдите площадь праллелограмма \(\displaystyle ABCD\small,\) если \(\displaystyle \angle CBY=30^{\circ}\small, AB=4\small, BX=5\small,\) а площадь четырехугольника \(\displaystyle YBXD\) равна \(\displaystyle 10\small.\)
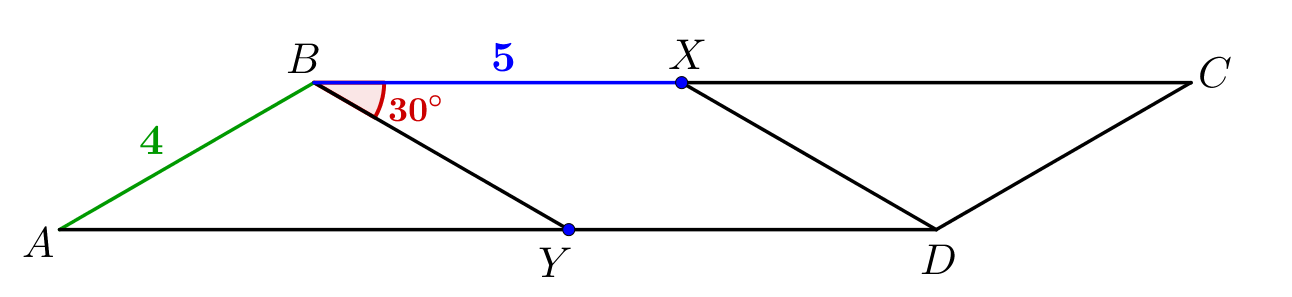
Отрезки \(\displaystyle BY\) и \(\displaystyle DX\) делят параллелограмм \(\displaystyle ABCD\) на
| 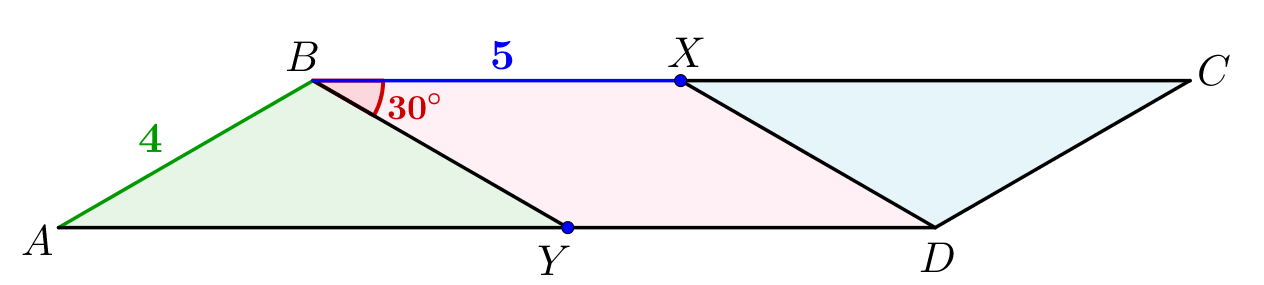 |
В \(\displaystyle BXDY\) известны площадь, сторона и угол. Доказав, что это параллелограмм, можно найти оставшуюся сторону.
Затем можно будет найти площади треугольников \(\displaystyle ABY\) и \(\displaystyle CDX\small.\)
\(\displaystyle S_{ABY}=4\sqrt{3}\small.\)
1. В четырехугольнике \(\displaystyle BXDY\) противоположные стороны параллельны. Значит, \(\displaystyle BXDY\) – параллелограмм. Найдем сторону \(\displaystyle BY\) этого параллелограмма. Запишем формулу площади параллелограмма и подставим известные значения: \(\displaystyle S_{BXDY}=BX\cdot BY\cdot\sin \angle XBY\small.\) \(\displaystyle 10=5\cdot BY\cdot\sin30^{\circ}\small.\) Откуда находим \(\displaystyle BY{\small:}\) \(\displaystyle BY=\frac{10}{5\sin30^{\circ}}=4\small.\) | 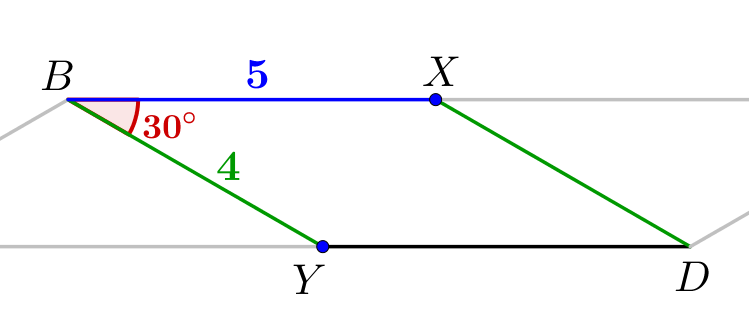 |
2. Тогда треугольник \(\displaystyle ABY\) равнобедренный и \(\displaystyle AB=BY=4\small.\) Найдем его углы. Прямые \(\displaystyle BC\) и \(\displaystyle AD\) параллельны, значит, \(\displaystyle \angle BYA=\angle CBY=30^{\circ}\small.\) И равные углы равнобедренного треугольника: \(\displaystyle \angle BAY=\angle BYA=30^{\circ}\small.\) Сумма углов треугольника равна \(\displaystyle 180^{\circ}\small,\) откуда третий угол треугольника \(\displaystyle \angle ABY=180^{\circ}-30^{\circ}-30^{\circ}=120^{\circ}\) Площадь треугольника равна половине произведения двух сторон и синуса угла между ними: \(\displaystyle S_{ABY}=\frac{AB\cdot BY\cdot\sin120^{\circ}}{2}=\frac{4\cdot4\cdot\frac{\sqrt{3}}{2}}{2}=4\sqrt{3}\small.\) | 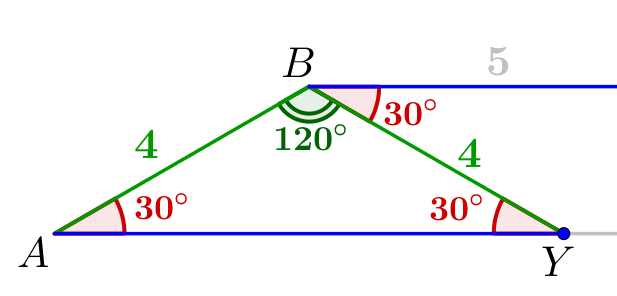 |
\(\displaystyle S_{XDC}=S_{ABY}=4\sqrt{3}\small.\)
Таким образом, получаем:
\(\displaystyle S_{ABCD}=S_{BXDY}+S_{XDC}+S_{ABY}=10+4\sqrt{3}+4\sqrt{3}=10+8\sqrt{3}\small.\)
Ответ: \(\displaystyle S_{ABCD}=10+8\sqrt{3}\small.\)