Угол \(\displaystyle A\) параллелограмма \(\displaystyle ABCD\) равен \(\displaystyle 30^{\circ}\small.\) Сторона \(\displaystyle AB=4\small,\) а его площадь равна \(\displaystyle 10\small.\) Найдите периметр \(\displaystyle ABCD\small.\)
Площадь параллелограмма равна произведению соседних сторон на синус угла между ними:
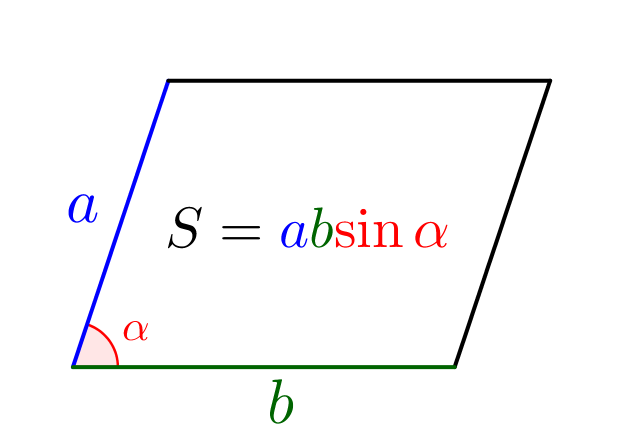
Используя формулу площади параллелограмма, найдем его вторую сторону.
Пусть неизвестная сторона \(\displaystyle b\small,\) тогда, подставляя \(\displaystyle S=10\small,a=4\) и \(\displaystyle \color{red}{\alpha}=30^{\circ}\small,\) получаем:
\(\displaystyle 10=4\cdot b\cdot\sin30^{\circ}\small,\)
\(\displaystyle 10=4b\cdot\frac{1}{2}\small,\)
\(\displaystyle b=5\small.\)
Периметр параллелограмма равен удвоенной сумме соседних сторон:
\(\displaystyle P=2\cdot(a+b)=2\cdot(4+5)=18\small.\)
Ответ: \(\displaystyle P=18\small.\)