Теория: Задачи-2 (короткая версия)

Задание

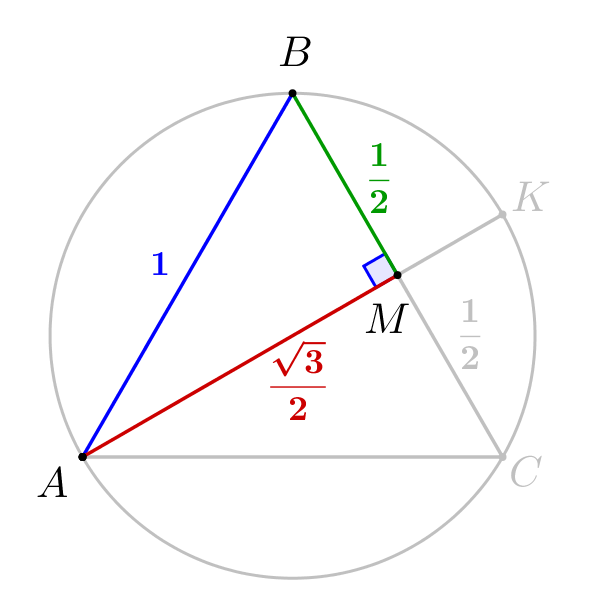
Биссектриса угла \(\displaystyle A\) равностороннего треугольника \(\displaystyle ABC\) пересекает описанную окружность в точке \(\displaystyle K\small.\) Точка \(\displaystyle M\) – середина стороны \(\displaystyle BC\small.\) Найдите \(\displaystyle KM\small,\) если \(\displaystyle AB=1\small.\)

\(\displaystyle KM=\)

\frac{\sqrt{3}}{6}

Решение

Правило

Теорема об отрезках пересекающихся хорд

Если две хорды окружности пересекаются, то произведение отрезков одной хорды равно произведению отрезков другой хорды:

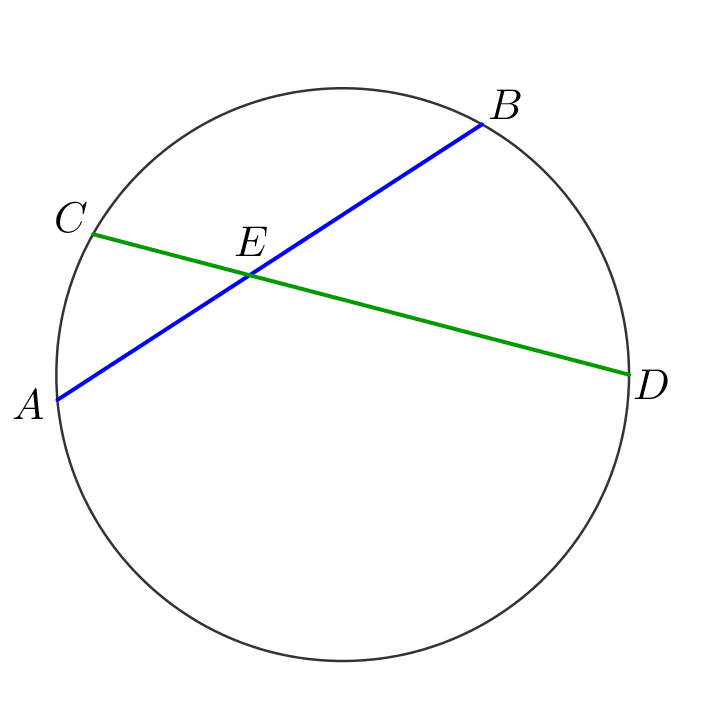
\(\displaystyle \color{blue}{AE}\cdot \color{blue}{BE}=\color{green}{CE}\cdot \color{green}{ DE}\)

Отрезок \(\displaystyle AM\) – биссектриса равностороннего треугольника, а значит, \(\displaystyle AM\) является и высотой, и медианой. То есть

\(\displaystyle CM=BM=\frac{1}{2}\small,\)
\(\displaystyle \angle AMB=90^{\circ}\small.\)

Тогда по теореме Пифагора найдем \(\displaystyle AM{\small:}\)

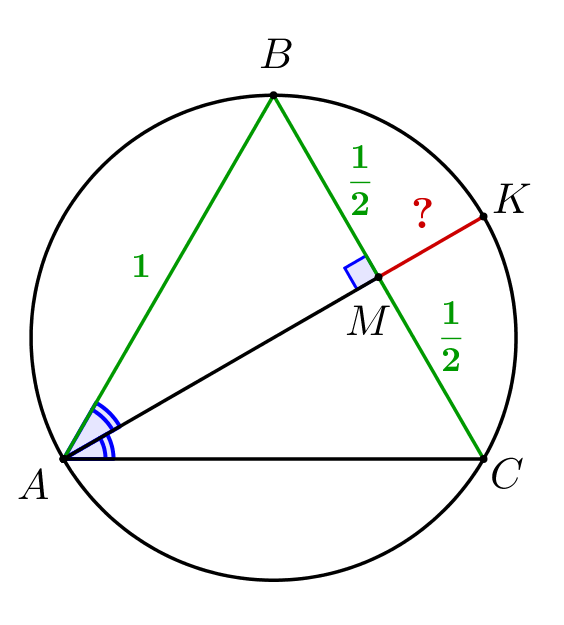\(\displaystyle AM=\frac{\sqrt{3}}{2}\small.\)

По теореме об отрезках пересекающихся хорд, получаем:

\(\displaystyle CM\cdot BM=AM\cdot KM\small.\)

Подставляя известные значения, получаем:

\(\displaystyle \frac{1}{2}\cdot\frac{1}{2}=\frac{\sqrt{3}}{2}\cdot KM\small,\)

\(\displaystyle KM=\frac{1}{2\sqrt{3}}=\frac{\sqrt{3}}{6}\small.\)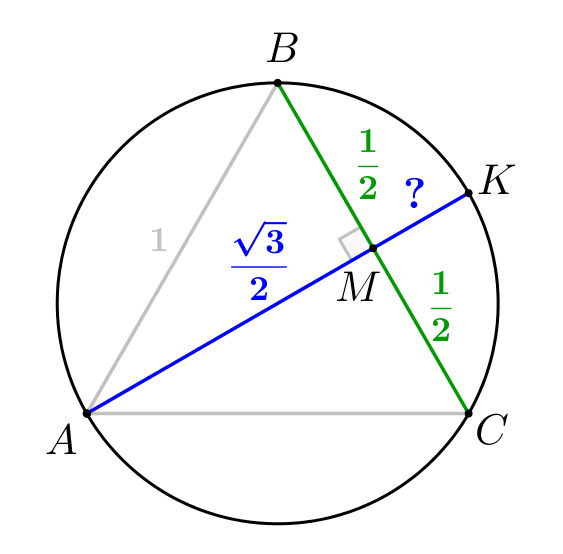

Ответ: \(\displaystyle KM=\frac{\sqrt{3}}{6}\small.\)