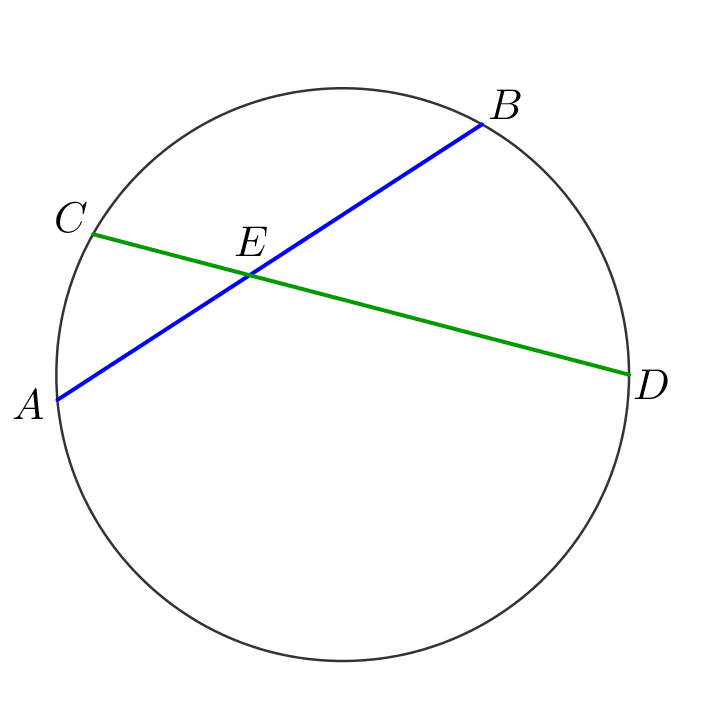
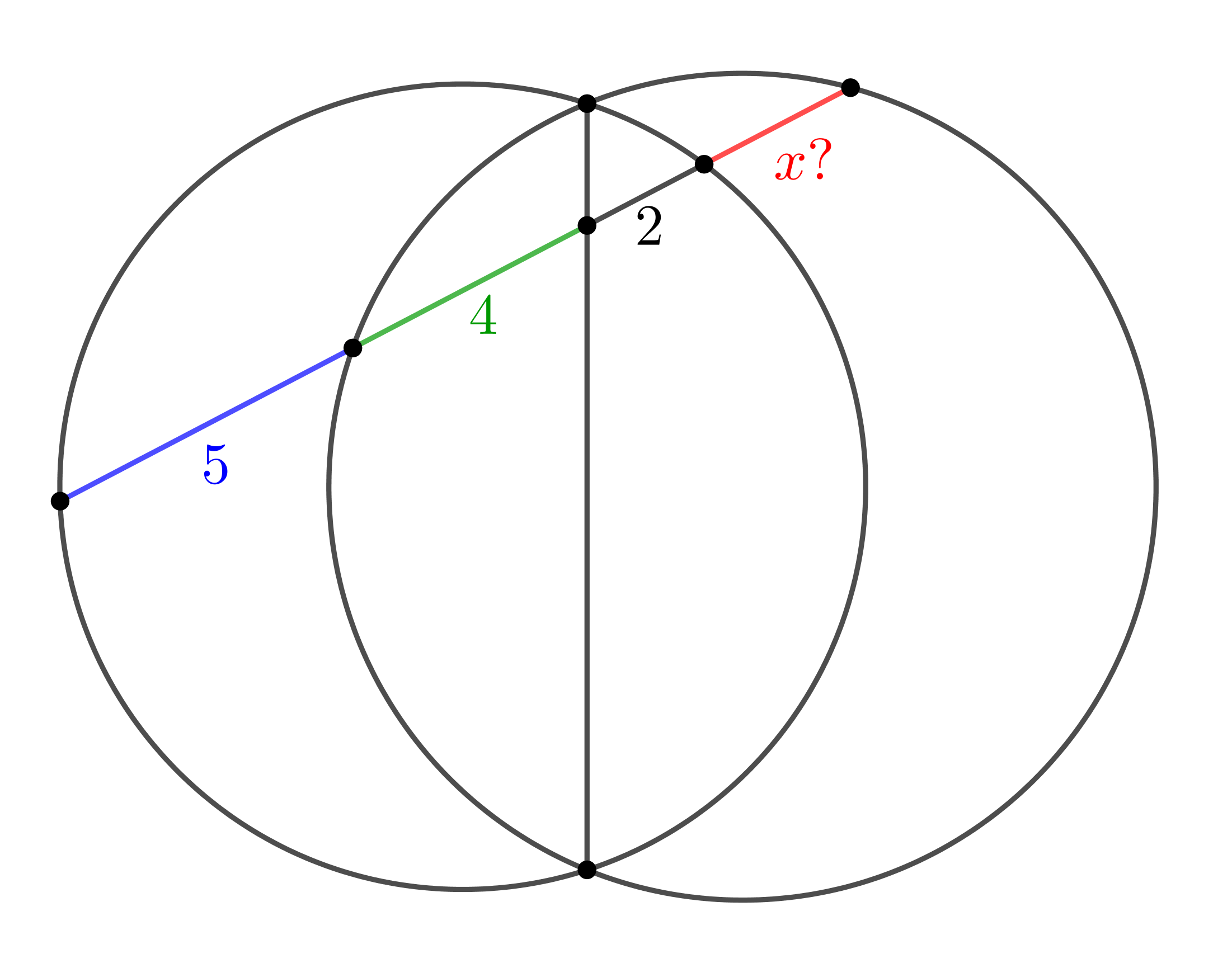
Прямая пересекает две окружности и их общую хорду в пяти точках. Три отрезка между этими точками на рисунке имеют длины \(\displaystyle 2, \,4\) и \(\displaystyle 5\small.\) Найдите длину четвертого отрезка.
Обозначим точки пересечения окружностей и отрезков:
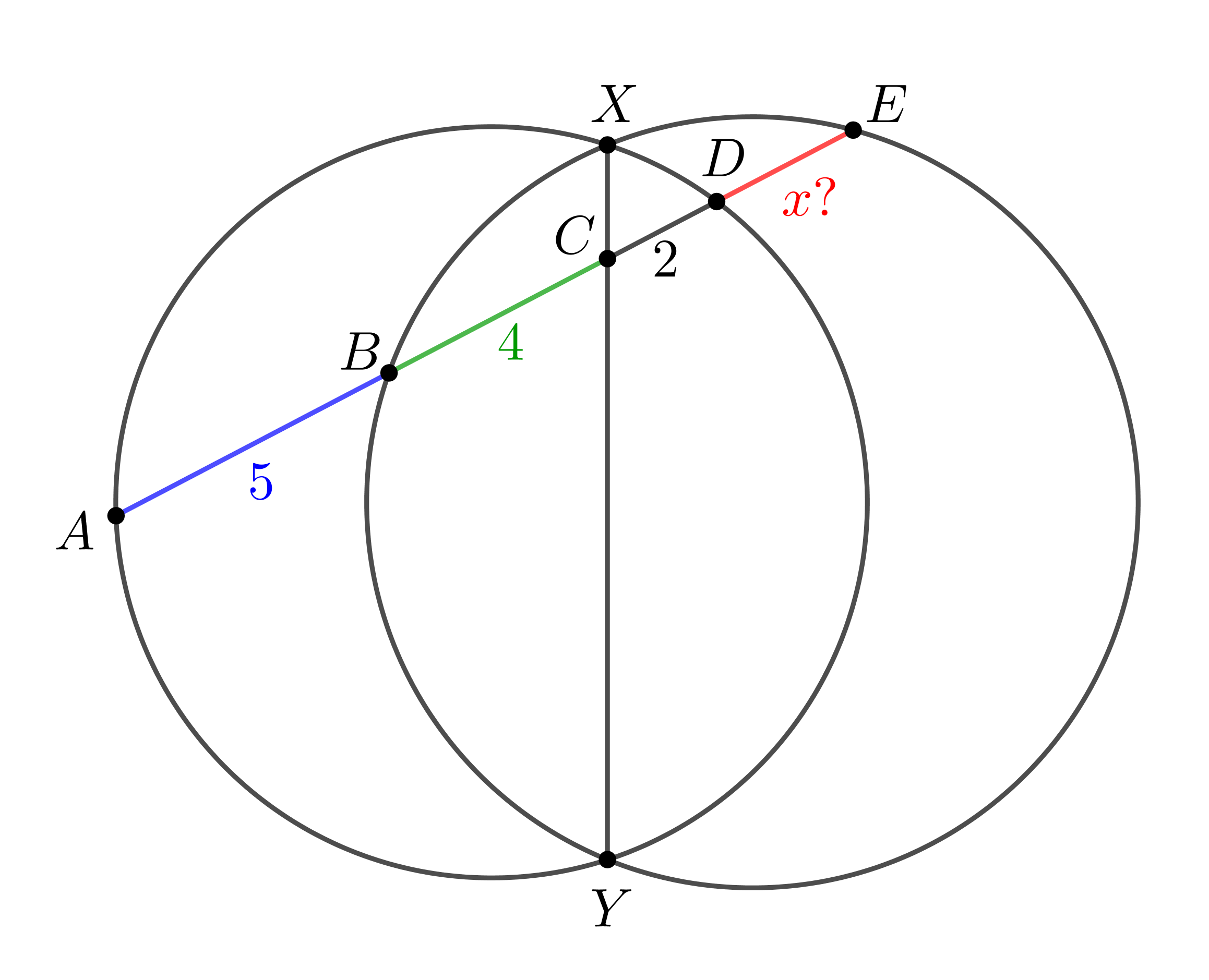
1. Для окружности, на которой лежат точки \(\displaystyle A,\,X,\,D,\,Y{\small:}\) \(\displaystyle AC\cdot CD=XC\cdot YC\small.\) Подставляя известные значения \(\displaystyle AC=9,\,CD=2{\small,}\) получаем: \(\displaystyle XC\cdot YC=9\cdot2=18\small.\) | 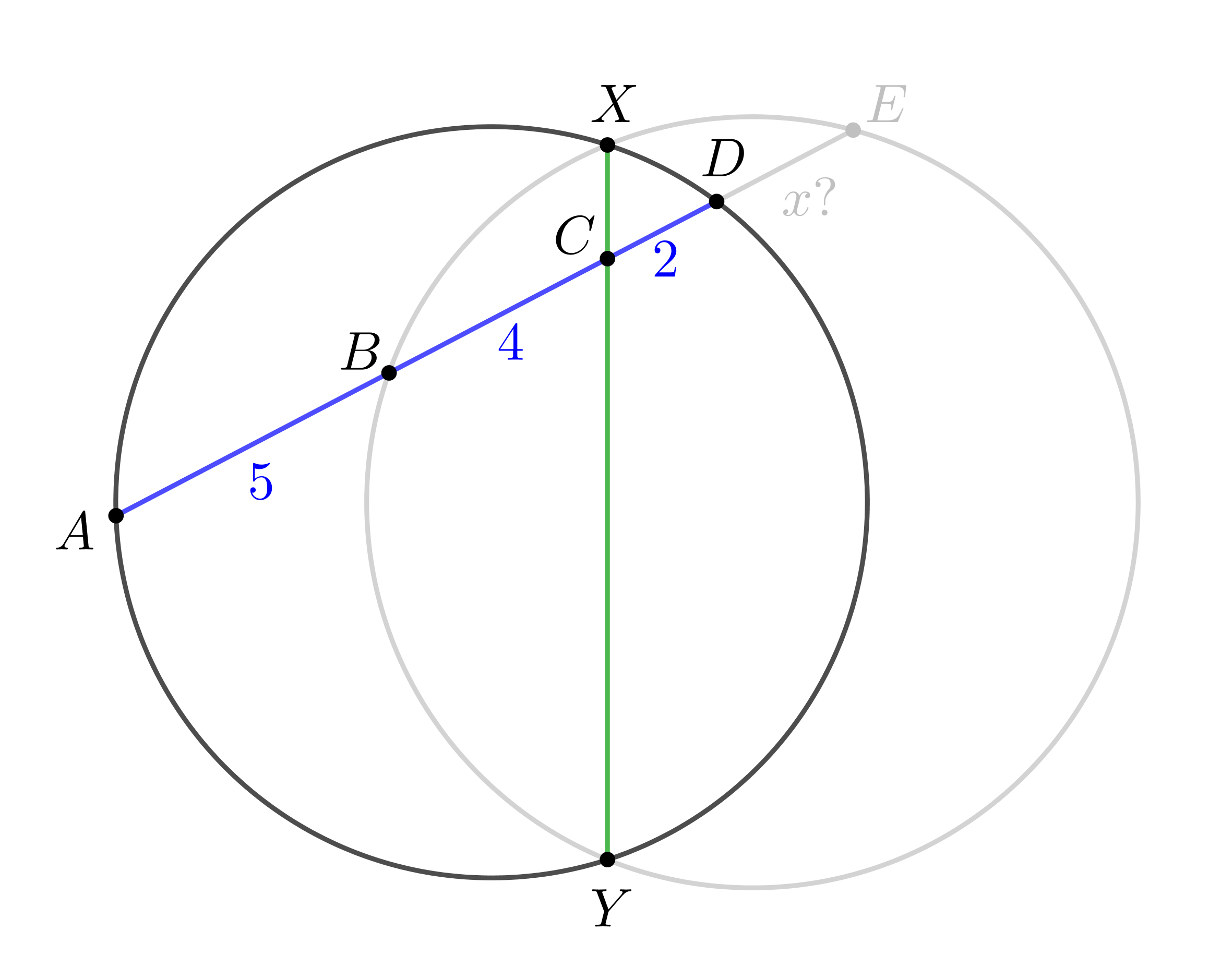 |
2. Для окружности, на которой лежат точки \(\displaystyle B,\,X,\,E,\,Y{\small:}\) \(\displaystyle BC\cdot CE=XC\cdot YC\small.\) Подставим \(\displaystyle XC\cdot YC=18\) и \(\displaystyle BC=4,\,CE=2+x\small,\) получаем: \(\displaystyle 4\cdot (2+x)=18\small.\) Откуда находим \(\displaystyle x{\small:}\) \(\displaystyle x=\frac{5}{2}\small.\) | 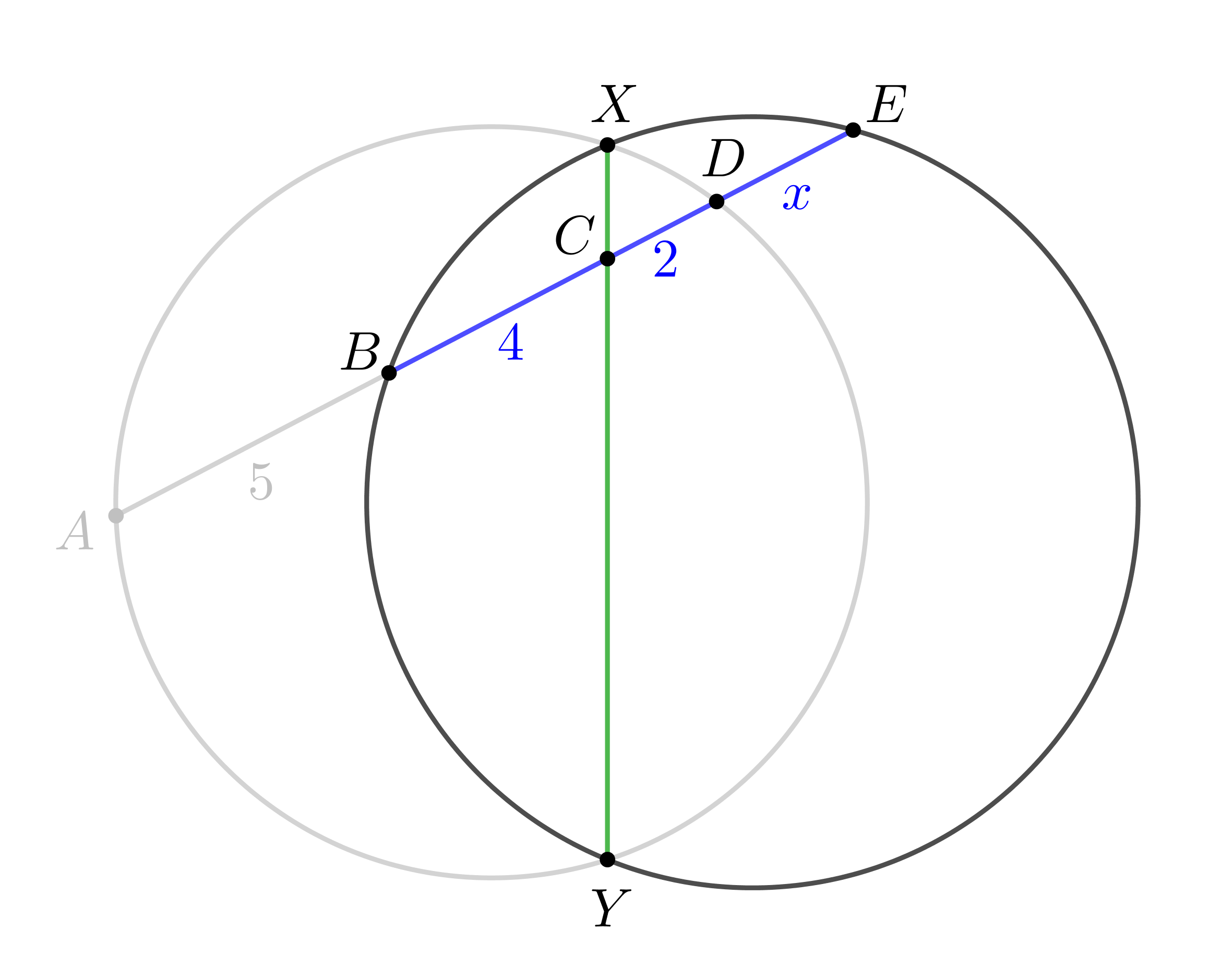 |
Ответ: \(\displaystyle x=\frac{5}{2}\small.\)