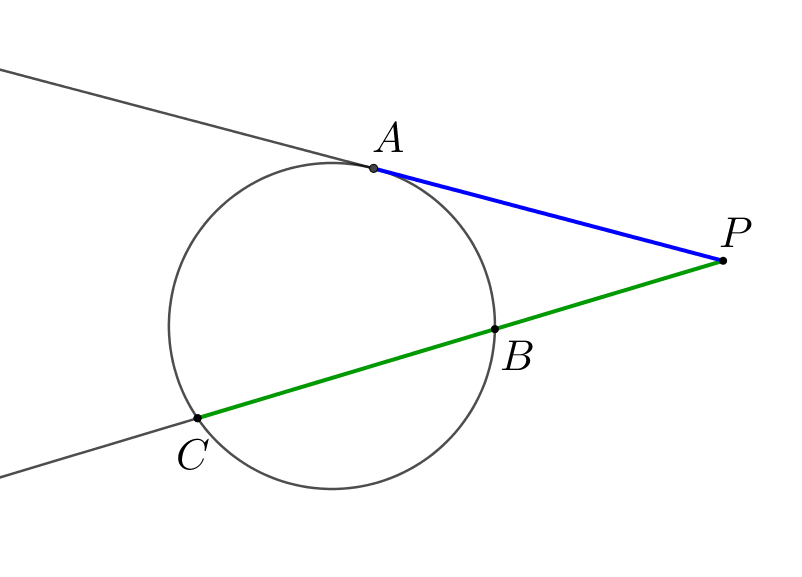
В угол вписаны две окружности. Первая имеет радиус \(\displaystyle 1\) и касается одной стороны угла в точке \(\displaystyle M\), вторая имеет радиус \(\displaystyle \sqrt{3}\) и касается другой стороны угла в точке \(\displaystyle K\small.\) Найдите отношение хорд, которые эти окружности высекают на прямой \(\displaystyle MK\small.\)
Обозначим оставшиеся точки касания прямых и окружностей, а также вершину угла:
Отрезки касательных, проведенных из одной точки, равны.
Тогда можно сразу отметить, что
\(\displaystyle ON=OM\) и \(\displaystyle OK=OL\small.\)
А значит, и
\(\displaystyle NK=ML\small.\)
Тогда для точки \(\displaystyle M\) и окружности радиуса \(\displaystyle \sqrt{3}{\small:}\)
\(\displaystyle ML^2=MY\cdot MK\small.\)
Для точки \(\displaystyle K\) и окружности радиуса \(\displaystyle 1\small,\) получаем:
\(\displaystyle KN^2=KX\cdot KM\small.\)
Поскольку \(\displaystyle ML=KN\small,\) то
\(\displaystyle MY\cdot MK=ML^2=KN^2=KX\cdot KM\small,\)
\(\displaystyle MY\cdot \cancel{MK}=KX\cdot \cancel{KM}\small,\)
\(\displaystyle MY=KX\small,\)
\(\displaystyle \frac{MY}{KX}=1\small.\)
Ответ: \(\displaystyle \frac{MY}{KX}=1\small.\)