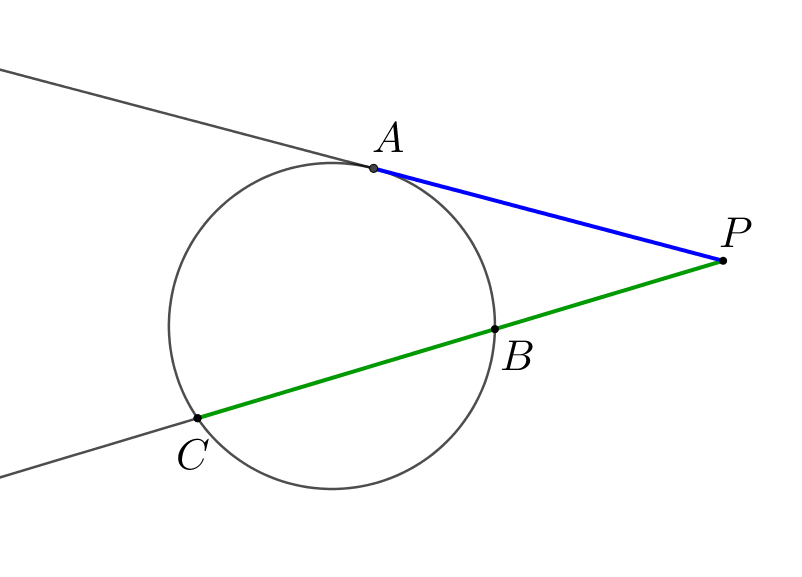
В прямоугольном треугольнике \(\displaystyle ABC\) катеты равны \(\displaystyle AB=6,\,AC=8\small.\) Вписанная окружность касается катета \(\displaystyle AB\) в точке \(\displaystyle L\small.\) Отрезок \(\displaystyle CL\) пересекает окружность второй раз в точке \(\displaystyle N\small.\) Найдите отношение
Сразу отметим, что в прямоугольном треугольнике с катетами \(\displaystyle 8\) и \(\displaystyle 6\) гипотенуза равна \(\displaystyle \sqrt{8^2+6^2}=10\small.\) | 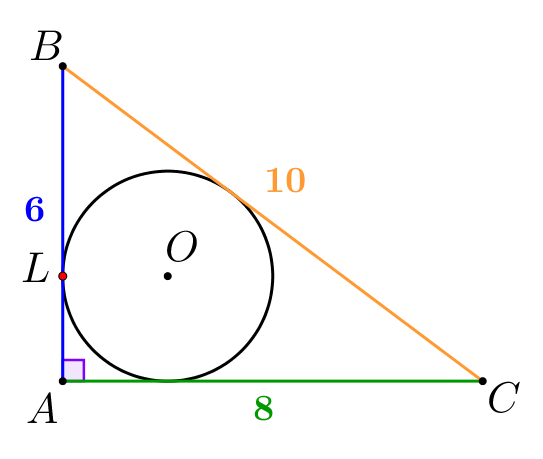 |
Тогда, чтобы решить задачу:
- найдем длины отрезков, на которые вписанная окружность делит стороны;
- найдем длину отрезка \(\displaystyle CL{\small;}\)
- найдем необходимое отношение отрезков.
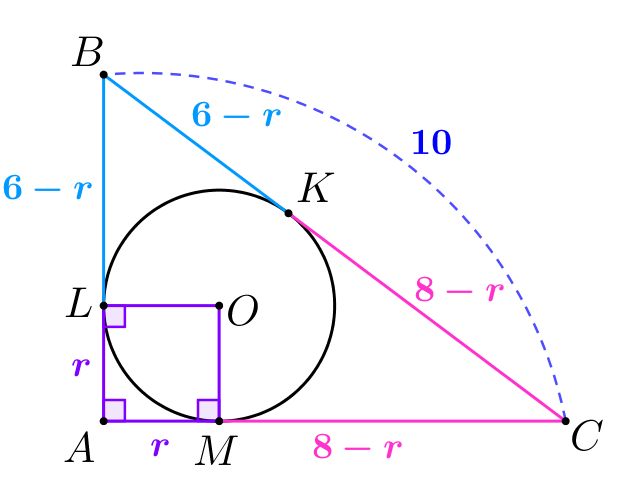
\(\displaystyle AL=AM=2\small,\) \(\displaystyle BL=BK=4\small,\) \(\displaystyle CM=CK=6\small.\)
Обозначим радиус вписанной окружности \(\displaystyle r\small.\) Отрезки касательных, проведенных из одной точки, равны. Тогда
Кроме этого, отрезки \(\displaystyle BK\) и \(\displaystyle CK\) в сумме дают гипотенузу \(\displaystyle BC\small{:}\) \(\displaystyle 6-r+8-r=10\small.\) Отсюда находим \(\displaystyle r=2\small.\) Тогда для всех отрезков касательных получаем:
|  |
\(\displaystyle CL=\sqrt{AL^2+AC^2}=\sqrt{2^2+8^2}=\sqrt{68}\small.\)
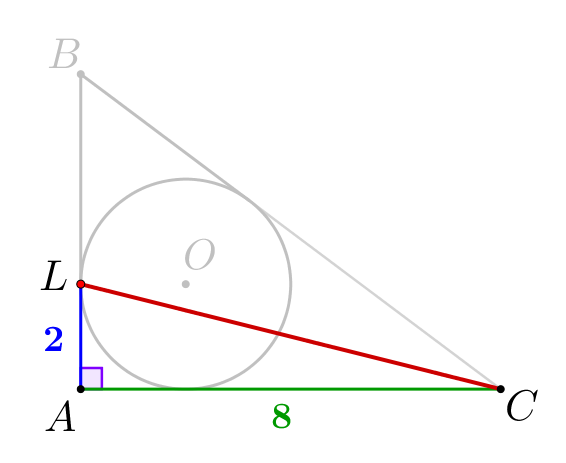
Для секущей \(\displaystyle CK\) и касательной \(\displaystyle CL\small{:}\) \(\displaystyle \color{blue}{CK^2}=\color{green}{CN}\cdot \color{green}{CL}\small,\) \(\displaystyle 6^2=CN \cdot \sqrt{68}\small,\) \(\displaystyle CN=\frac{36}{\sqrt{68}}\small.\) | 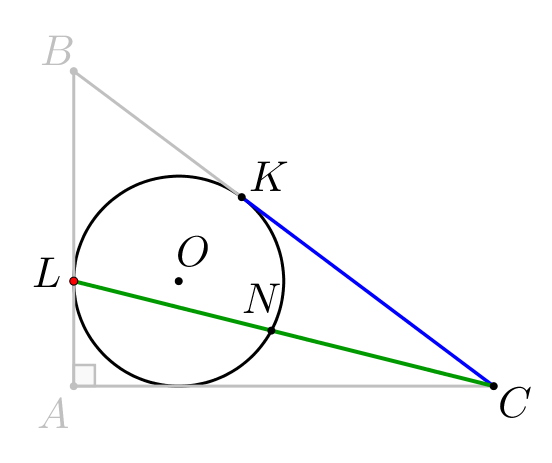 |
Тогда
\(\displaystyle NL=CL-CN=\sqrt{68}-\frac{36}{\sqrt{68}}=\frac{32}{\sqrt{68}}\small.\)
Теперь найдем отношение длин отрезков \(\displaystyle CN\) и \(\displaystyle NL\small{:}\)
\(\displaystyle \frac{CN}{NL}=\frac{36}{\sqrt{68}}:\frac{32}{\sqrt{68}}=\frac{36}{32}=\frac{9}{8}\small.\)
Ответ: \(\displaystyle \frac{CN}{NL}=\frac{9}{8}\small.\)