Окружность радиуса \(\displaystyle 1\) касается двух катетов прямоугольного треугольника и делит его гипотенузу на три равные части. Найдите площадь этого треугольника.
\(\displaystyle S=\)
Обозначим вершины треугольника, а также точки касания и пересечения сторон треугольника и окружности.
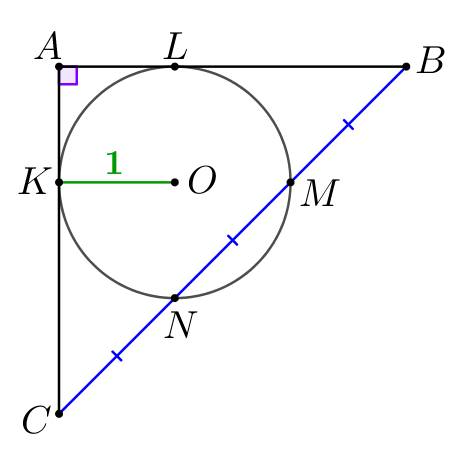
Чтобы найти площадь прямоугольного треугольника, найдем его катеты.
Так как касательные перпендикулярны радиусу, то в четырехугольнике \(\displaystyle OKAL\) есть минимум четыре прямых угла: \(\displaystyle \angle KAL=\angle ALO=\angle AKO=90^{\circ}\small.\) То есть \(\displaystyle OKAL\) – прямоугольник. Отрезки \(\displaystyle OK\) и \(\displaystyle OL\) – радиусы: \(\displaystyle OK=OL=1\small.\) Значит, \(\displaystyle OKAL\) – квадрат со стороной \(\displaystyle 1\) и \(\displaystyle AK=AL=1\small.\) | 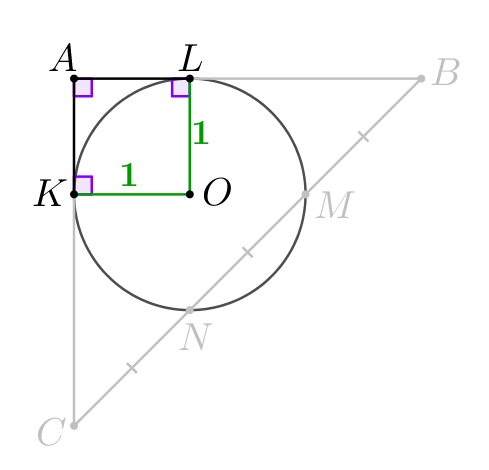 |
\(\displaystyle CK=BL=2\small.\)
Обозначим треть гипотенузы за \(\displaystyle x{\small:}\) \(\displaystyle CN=NM=BM=x\small.\) Воспользуемся тем, что произведение отрезков секущих равно квадрату касательной. Тогда для точки \(\displaystyle C\) и окружности получаем: \(\displaystyle CK^2=CN\cdot CM=x\cdot2x=2x^2\small,\) \(\displaystyle CK=x\sqrt{2}\small.\) И для точки \(\displaystyle B\) получаем: \(\displaystyle BL^2=BM\cdot BN=x\cdot2x=2x^2\small,\) \(\displaystyle BL=x\sqrt{2}\small.\) | 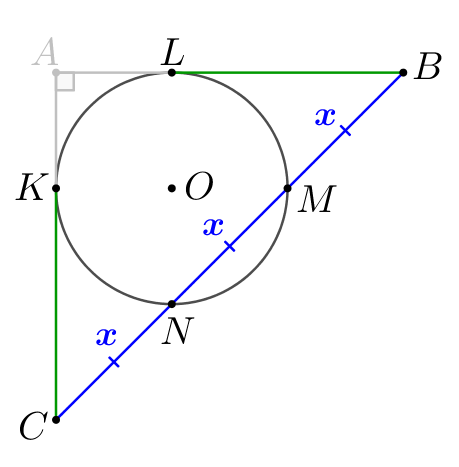 |
Значит, в прямоугольном треугольнике \(\displaystyle ABC{\small:}\)
| 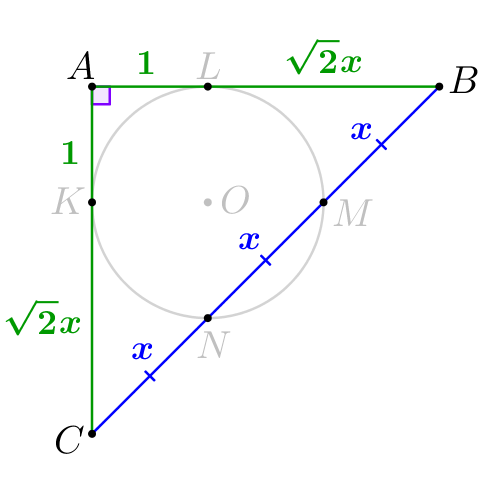 |
Тогда по теореме Пифагора:
\(\displaystyle (3x)^2=\left(1+x\sqrt{2}\right)^2+\left(1+x\sqrt{2}\right)^2\small,\)
\(\displaystyle (3x)^2=2\left(1+x\sqrt{2}\right)^2\small.\)
Длины отрезков положительны, поэтому извлечем квадратный корень из обеих частей и найдем \(\displaystyle x{\small:}\)
\(\displaystyle 3x=\sqrt{2}\left(1+x\sqrt{2}\right)\small,\)
\(\displaystyle 3x=\sqrt{2}+2x\small,\)
\(\displaystyle x=\sqrt{2}\small.\)
Тогда
\(\displaystyle CK=BL=x\sqrt{2}=2\small.\)
Получаем, что катеты треугольника \(\displaystyle ABC{\small:}\)
\(\displaystyle AC=AB=AL+LB=1+2=3\small.\)
Тогда его площадь равна:
\(\displaystyle S_{ABC}=\frac{AB\cdot AC}{2}=\frac{3\cdot3}{2}=4{,}5\small.\)
Ответ: \(\displaystyle 4{,}5\small.\)