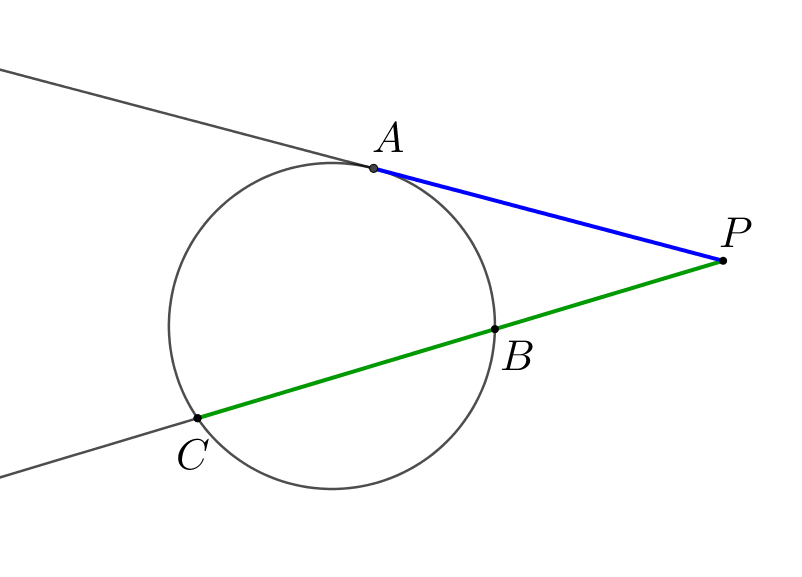
Окружность, вписанная в треугольник \(\displaystyle ABC\small,\) делит его медиану \(\displaystyle BM\) на три равные части. Найдите отношение сторон \(\displaystyle AB\) и \(\displaystyle AC\small,\) если точка касания окружности и стороны \(\displaystyle AC\) лежит на \(\displaystyle AM\small.\)
Обозначим точки касания окружностью сторон и точки пересечения медианы и окружности.
1. Покажем, что отрезки \(\displaystyle BL\) и \(\displaystyle MN\) равны.
Тогда для точки \(\displaystyle B\) и окружности получаем: \(\displaystyle BL^2=BX\cdot BY\small.\) А для точки \(\displaystyle M{\small:}\) \(\displaystyle MN^2=MY\cdot MX\small.\) | 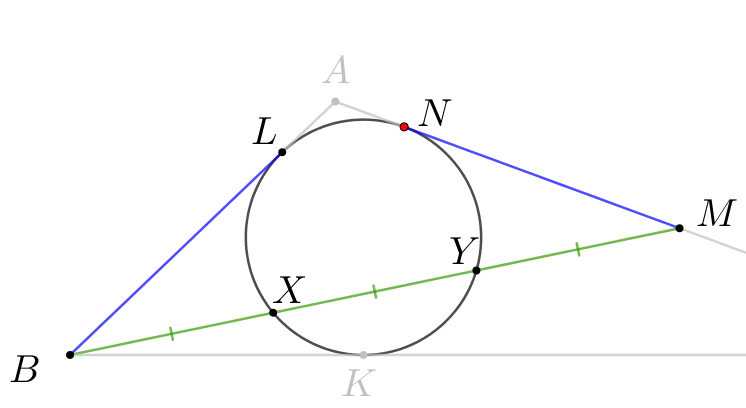 |
По условию \(\displaystyle BY=MX\) и \(\displaystyle BX=MY\small,\) значит,
\(\displaystyle BL^2=BX\cdot BY=MY\cdot MX=MN^2\small,\)
\(\displaystyle BL=MN\small.\)
2. Найдем отношение \(\displaystyle AC\) к \(\displaystyle AB\small.\)
Отрезки касательных из одной точки \(\displaystyle AL\) и \(\displaystyle AN\) равны. Тогда \(\displaystyle BA=BL+LA=MN+NA=AM\small.\) | 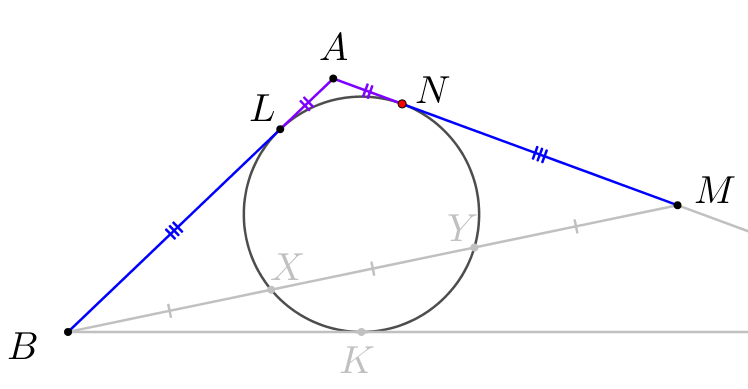 |
Отрезок \(\displaystyle BM\) – медиана треугольника. Тогда
\(\displaystyle AC=2AM=2AB\small,\)
\(\displaystyle \frac{AC}{AB}=2\small.\)
Ответ: \(\displaystyle \frac{AC}{AB}=2\small.\)