Окружность, вписанная в треугольник \(\displaystyle ABC\small,\) делит его медиану \(\displaystyle BM\) на три равные части. Найдите отношение сторон \(\displaystyle AC\) и \(\displaystyle AB\small,\) если точка касания окружности и стороны \(\displaystyle AC\) лежит на \(\displaystyle CM\small.\)
Напомним формулу длины медианы:
\(\displaystyle BM^2=\frac{2AB^2+2BC^2-AC^2}{4}\small.\)
Обозначим точки касания окружностью сторон и точки пересечения медианы и окружности.
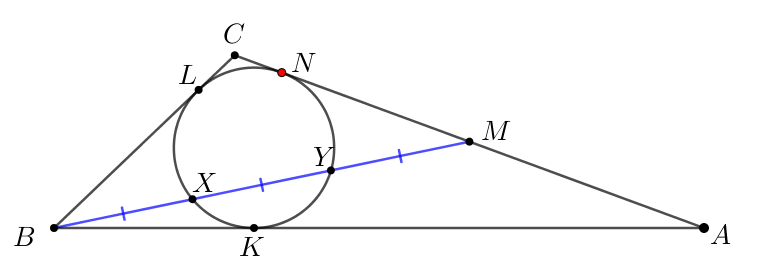
Чтобы решить задачу, поступим следующим образом:
- обозначим длину отрезка \(\displaystyle BX\) за \(\displaystyle x{ \small ,}\) а длину отрезка \(\displaystyle CN\) за \(\displaystyle y{\small ; }\)
- выразим стороны треугольника \(\displaystyle ABC \) через \(\displaystyle x \) и \(\displaystyle y{\small ; } \)
- используя формулу для медианы треугольника, выразим \(\displaystyle y \) через \(\displaystyle x{\small ; } \)
- найдем отношение \(\displaystyle AC \) к \(\displaystyle AB{ \small ,} \) используя их выражения через \(\displaystyle x \) и \(\displaystyle y{\small . } \)
\(\displaystyle BL=MN=x\sqrt{2}\)
Воспользуемся тем, что произведение отрезков секущих равно квадрату касательной.
Тогда для точки \(\displaystyle B\) и окружности получаем:
\(\displaystyle BL^2=BX\cdot BY=x\cdot2x\small,\)
\(\displaystyle BL=x\sqrt{2}\small.\)
И для точки \(\displaystyle M{\small:}\)
\(\displaystyle MN^2=MY\cdot MX=x\cdot2x\small.\)
\(\displaystyle MN=x\sqrt{2}\small.\)
\(\displaystyle AB=y+3x\sqrt{2},\,AC=2(x\sqrt{2}+y),\,BC=y+x\sqrt{2}\small.\)
Будем пользоваться тем, что отрезки касательных равны.
Тогда
\(\displaystyle CL=CN=y\) и \(\displaystyle BL=BK=x\sqrt{2}\small.\)
Точка \(\displaystyle M\) – середина \(\displaystyle AC\small,\) значит,
\(\displaystyle AM=CM=y+x\sqrt{2}\small.\)
Отрезки касательных \(\displaystyle AN\) и \(\displaystyle AK\) равны, то есть
\(\displaystyle AK=AN=AM+MN=y+2x\sqrt{2}\small.\)
Теперь можно найти все стороны треугольника:
\(\displaystyle AB=y+3x\sqrt{2},\,AC=2(x\sqrt{2}+y),\,BC=y+x\sqrt{2}\small.\)
\(\displaystyle y=\frac{x}{2\sqrt{2}}\small.\)
Запишем формулу медианы для треугольника \(\displaystyle ABC{\small:}\)
\(\displaystyle BM^2=\frac{2AB^2+2BC^2-AC^2}{4}\small.\)
Подставим длины отрезков:
\(\displaystyle (3x)^2=\frac{2(y+3x\sqrt{2})^2+2(y+x\sqrt{2})^2-(2(x\sqrt{2}+y))^2}{4}\small.\)
Раскроем скобки и приведем подобные слагаемые:
\(\displaystyle 9x^2=\frac{(\cancel{2y^2}+12xy\sqrt{2}+36x^2)+(\cancel{2y^2}+4xy\sqrt{2}+4x^2)-(\cancel{4y^2}+8xy\sqrt{2}+8x^2)}{4}\small,\)
\(\displaystyle 9x^2=\frac{8xy\sqrt{2}+32x^2}{4}\small,\)
\(\displaystyle 9x^2=2xy\sqrt{2}+8x^2\small.\)
Откуда выражаем
\(\displaystyle y=\frac{x}{2\sqrt{2}}\small.\)
\(\displaystyle \frac{AC}{AB}=\frac{2x\sqrt{2}+2y}{y+3x\sqrt{2}}=\frac{2x\sqrt{2}+\frac{2x}{2\sqrt{2}}}{\frac{x}{2\sqrt{2}}+3x\sqrt{2}}=\frac{10}{13}\small.\)
Ответ:\(\displaystyle \frac{AC}{AB}=\frac{10}{13}\small.\)