Известны длины векторов \(\displaystyle \vec{a}=3\) и \(\displaystyle \vec{b}=4\small.\) Какие значения может принимать длина вектора \(\displaystyle \vec{a}+\vec{b}?\)
Обозначим сумму векторов \(\displaystyle \vec{a}\) и \(\displaystyle \vec{b}{\small:}\) \(\displaystyle \vec{c}=\vec{a}+\vec{b}\small.\)
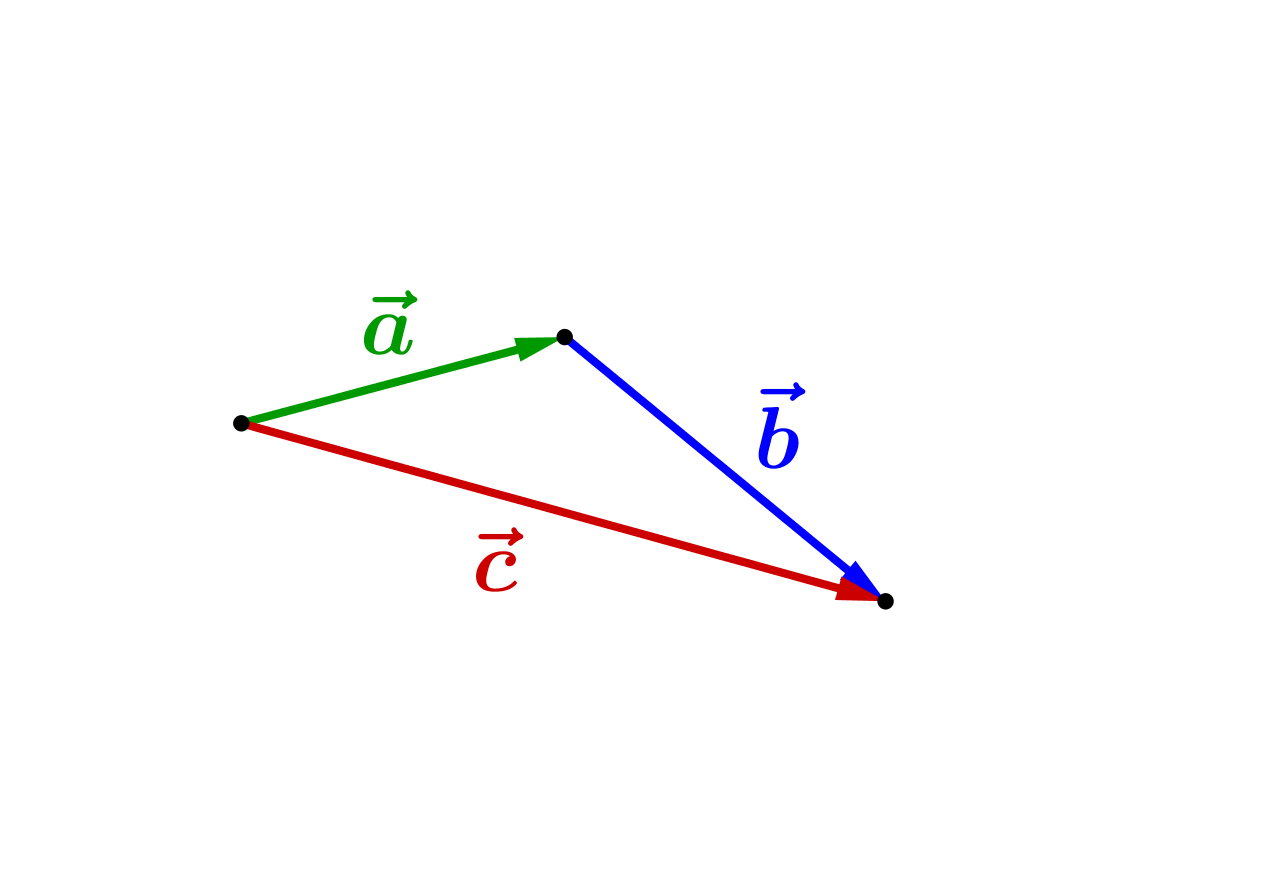
По правилу сложения векторов \(\displaystyle \vec{a},\,\vec{b}\) и \(\displaystyle \vec{c}\) образуют треугольник или лежат на одной прямой:
| Случай 1 | Случай 2 | Случай 3 |
 |
В первом случае \(\displaystyle |\vec{c}|=|\vec{b}|-|\vec{a}|=4-3=1\small.\)
Во втором случае \(\displaystyle |\vec{c}|=|\vec{b}|+|\vec{a}|=4+3=7\small.\)
В третьем случае длины векторов \(\displaystyle \vec{a},\,\vec{b}\) и \(\displaystyle \vec{c}\) – длины сторон треугольника. Значит, для \(\displaystyle |\vec{a}|,\,|\vec{b}|\) и \(\displaystyle |\vec{c}|\) выполняются неравенства треугольника.
Тогда
\(\displaystyle |\vec{c}|+3>4\) и \(\displaystyle 3+4>|\vec{c}|\small.\)
То есть
\(\displaystyle 1<|\vec{c}|<7\small.\)
Для такого \(\displaystyle \vec{c}\) все неравенства треугольника выполняются. Значит, треугольник со сторонами \(\displaystyle |\vec{a}|,\,|\vec{b}|\) и \(\displaystyle |\vec{c}|\) существует.
Объединяя все три случая, получаем:
\(\displaystyle 1\leqslant|\vec{a}+\vec{b}|\leqslant7\small.\)