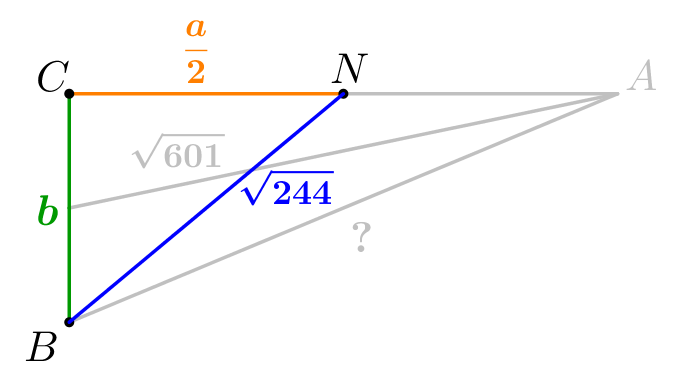
Медианы, проведенные к катетам прямоугольного треугольника, равны \(\displaystyle \sqrt{601}\) и \(\displaystyle \sqrt{244}\small.\) Найдите гипотенузу треугольника.
Обозначим длины катетов \(\displaystyle AC=a\) и \(\displaystyle BC=b\small.\) Тогда \(\displaystyle BM=CM=\frac{b}{2}\) и \(\displaystyle AN=CN=\frac{a}{2}\small.\) | 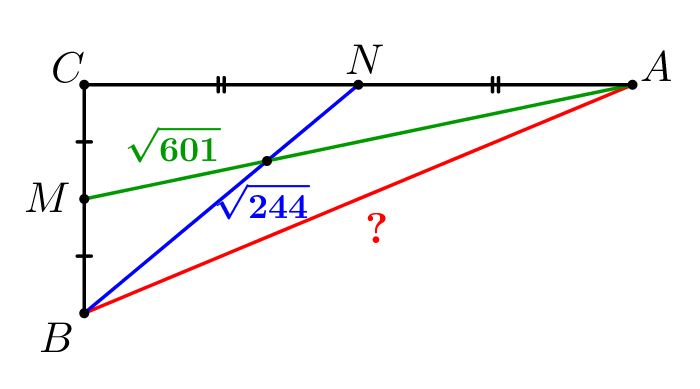 |
Чтобы решить задачу:
- выразим длины медиан через \(\displaystyle a\) и \(\displaystyle b\small,\)
- найдем \(\displaystyle a\) и \(\displaystyle b\small,\)
- найдем гипотенузу \(\displaystyle AB\) по теореме Пифагора.
1. По теореме Пифагора сумма квадратов катетов прямоугольного треугольника равна квадрату гипотенузы.
\(\displaystyle 2404=b^2+4a^2\small.\)
По теореме Пифагора: \(\displaystyle MA^2=MC^2+AC^2\small,\) \(\displaystyle (\sqrt{601})^2=\left(\frac{b}{2}\right)^2+a^2\small,\) \(\displaystyle 601=\frac{b^2}{4}+a^2\small.\) Чтобы избавиться от дробей, умножим обе части на \(\displaystyle 4{\small:}\) \(\displaystyle 2404=b^2+4a^2\small.\) | 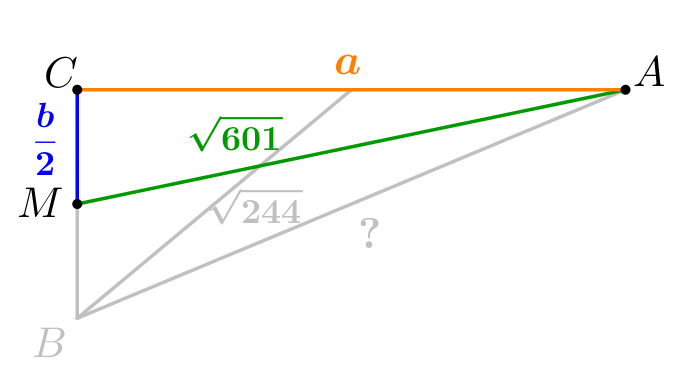 |
\(\displaystyle 976=a^2+4b^2\small.\)
\(\displaystyle\begin{cases}b^2+4a^2=2404\small,\\a^2+4b^2=976\small.\end{cases}\)
Получаем:
\(\displaystyle a^2=576\) и \(\displaystyle b^2=100\small.\)
3. Найдем гипотенузу прямоугольного треугольника \(\displaystyle ABC\small,\) используя теорему Пифагора:
\(\displaystyle AB^2=AC^2+BC^2=a^2+b^2=576+100=676\small,\)
\(\displaystyle AB=\sqrt{676}=26\small.\)
Ответ: \(\displaystyle 26\small.\)