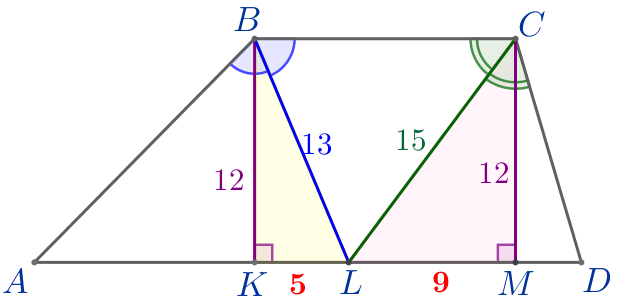
Точка пересечения биссектрис тупых углов при основании \(\displaystyle BC\) трапеции \(\displaystyle ABCD\) лежит на другом ее основании. Найдите все стороны трапеции, если ее высота равна \(\displaystyle 12\small,\) а биссектрисы \(\displaystyle BL\) и \(\displaystyle CL\) равны соответственно \(\displaystyle 13\) и \(\displaystyle 15\small.\)
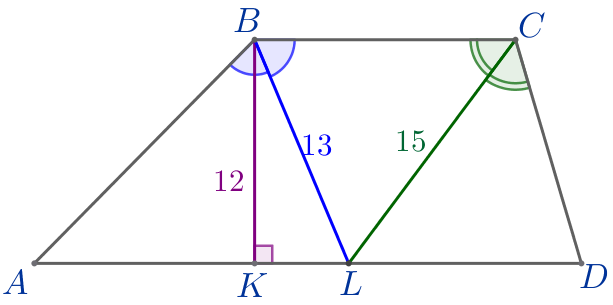
Выполним дополнительное построение.
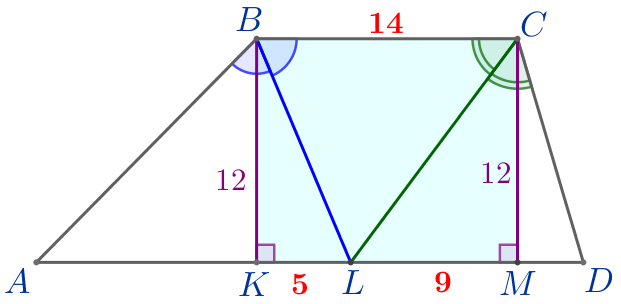
Из точки \(\displaystyle C\) проведем высоту \(\displaystyle CM\) трапеции \(\displaystyle ABCD{\small.}\)
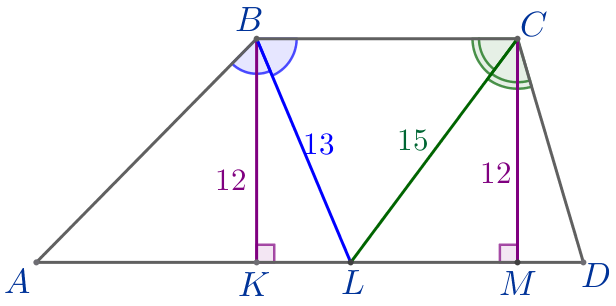
1. Найдем длины отрезков \(\displaystyle KL{\small,}\) \(\displaystyle ML\) и \(\displaystyle BC{\small.}\)
\(\displaystyle KL=5{\small;}\)
\(\displaystyle ML=9{\small.}\)
\(\displaystyle BC=14{\small.}\)
Так как основания трапеции параллельны \(\displaystyle (BC \parallel AD){\small,}\) то
- \(\displaystyle \angle ALB=\angle CBL\) – накрест лежащие при секущей \(\displaystyle BL{\small.}\)
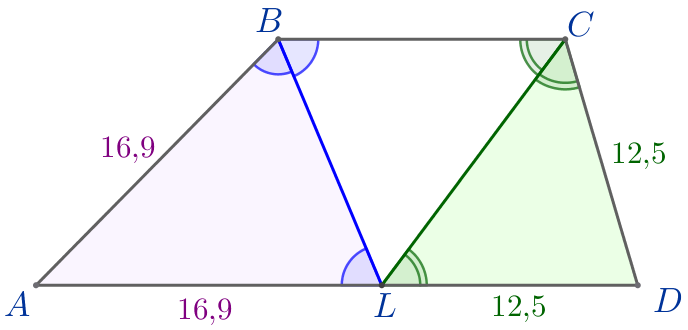
Следовательно, \(\displaystyle \angle ALB=\angle ABL\) и \(\displaystyle \triangle ABL\) – равнобедренный.
- \(\displaystyle \angle DLC=\angle BCL\) – накрест лежащие при секущей \(\displaystyle CL{\small.}\)
Следовательно, \(\displaystyle \angle DLC=\angle DCL\) и \(\displaystyle \triangle CDL\) – равнобедренный.
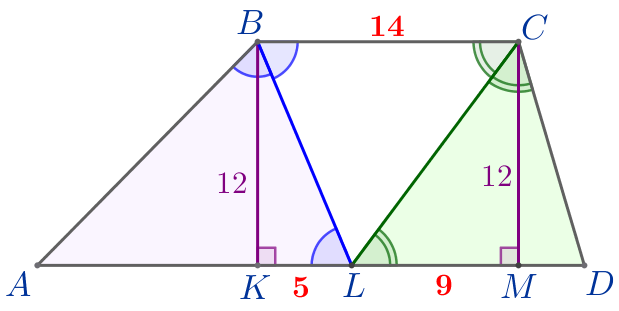
2. Найдем \(\displaystyle AB,\,CD\) и \(\displaystyle AD{\small.}\)
\(\displaystyle AB=16{,}9\small.\)
Обозначим длину неизвестной стороны \(\displaystyle AB\) за \(\displaystyle x\small.\)
Так как треугольник \(\displaystyle ABL\) – равнобедренный, то \(\displaystyle AL=AB=x\small.\) Тогда
\(\displaystyle AK=x-5\small.\)
По теореме Пифагора для треугольника \(\displaystyle ABK\small:\) \(\displaystyle AB^2=BK^2+AK^2\small;\) \(\displaystyle x^2=12^2+(x-5)^2\small.\) Найдем \(\displaystyle x{\small:}\) \(\displaystyle x^2=144+(x^2-10x+25)\small;\) \(\displaystyle 0=144+25-10x\small;\) \(\displaystyle x=16{,}9\small.\) | 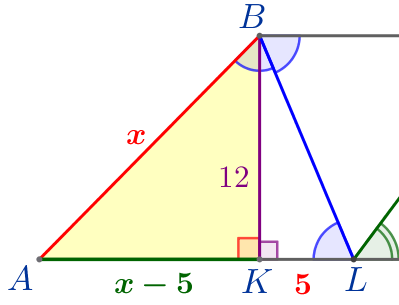 |
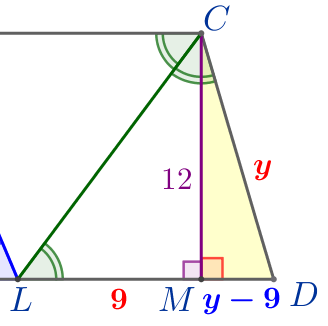
\(\displaystyle CD=12{,}5\small.\)
\(\displaystyle AD=29{,}4\small.\)
Ответ: \(\displaystyle AB=16{,}9{\small ; }\, \, \, BC=14{\small ; }\, \, \, CD=12{,}5{\small ; }\, \, \, AD=29{,}4\small.\)