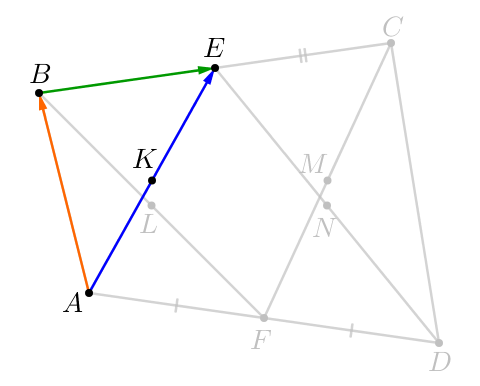
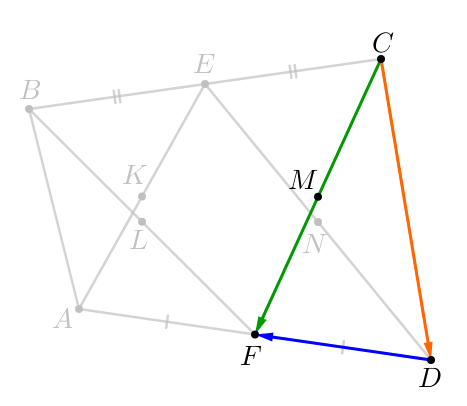
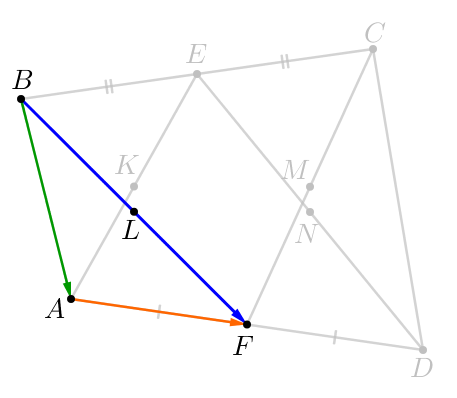
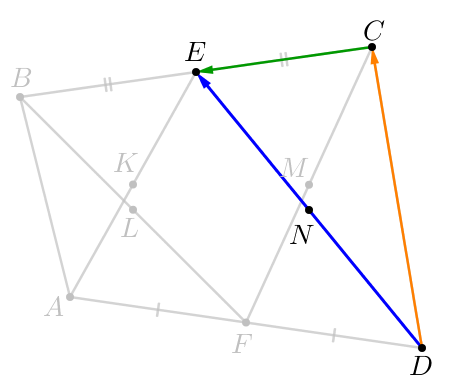
В четырёхугольнике \(\displaystyle ABCD\) точки \(\displaystyle E\) и \(\displaystyle F\) — середины непараллельных сторон \(\displaystyle BC\) и \(\displaystyle AD\small.\) Точки \(\displaystyle K,\,L,\,M,\,N\) – середины отрезков \(\displaystyle AE,\,BF,\,CF\) и \(\displaystyle ED\) соответственно.
Выразите векторы \(\displaystyle \overrightarrow{KM}\) и \(\displaystyle \overrightarrow{LN}\) через векторы, соответствующие сторонам четырехугольника \(\displaystyle ABCD{\small:}\)
Что можно сказать про четырехугольник \(\displaystyle KMNL?\)
Четырехугольник \(\displaystyle KMNL\) является
Отметим, что векторы \(\displaystyle \overrightarrow{AE},\,\overrightarrow{BF},\,\overrightarrow{CF}\) и \(\displaystyle \overrightarrow{DE}\) можно выразить через векторы, соответствющие сторонам \(\displaystyle \overrightarrow{AB},\,\overrightarrow{BC},\,\overrightarrow{CD}\) и \(\displaystyle \overrightarrow{DA}\small.\)
Затем через эти \(\displaystyle 8\) векторов несложно выразить и векторы \(\displaystyle \overrightarrow{KM}\) и \(\displaystyle \overrightarrow{LN}\small.\)
Проделаем вычисления.
1. Чтобы получить вектор \(\displaystyle \overrightarrow{KM}\small,\) выразим векторы \(\displaystyle \overrightarrow{KE}\) и \(\displaystyle \overrightarrow{CM}\) через стороны четырехугольника.
| \(\displaystyle \overrightarrow{KM}=\overrightarrow{KE}+\frac{\overrightarrow{BC}}{2}+\overrightarrow{CM}\small.\) | 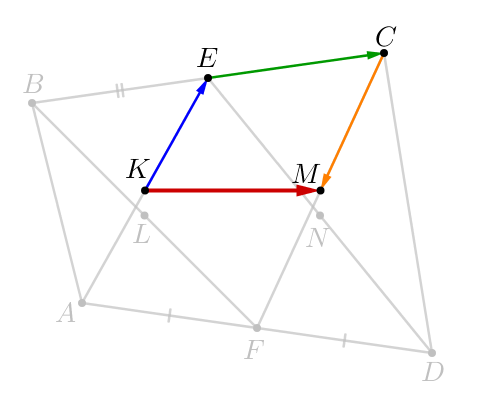 |
\(\displaystyle \overrightarrow{KE}=\frac{\overrightarrow{AB}}{2}+\frac{\overrightarrow{BC}}{4}\small.\)
\(\displaystyle \overrightarrow{CM}=\frac{\overrightarrow{CD}}{2}+\frac{\overrightarrow{DA}}{4}\small.\)
Тогда
\(\displaystyle \begin{aligned}\overrightarrow{KM}=\overrightarrow{KE}+\frac{\overrightarrow{BC}}{2}+\overrightarrow{CM}=\frac{\overrightarrow{AB}}{2}+\frac{\overrightarrow{BC}}{4}+\frac{\overrightarrow{BC}}{2}+\frac{\overrightarrow{CD}}{2}+\frac{\overrightarrow{DA}}{4}=\\=\frac{1}{2}\overrightarrow{AB}+\frac{3}{4}\overrightarrow{BC}+\frac{1}{2}\overrightarrow{CD}+\frac{1}{4}\overrightarrow{DA}\end{aligned}\small.\)
2. Чтобы получить вектор \(\displaystyle \overrightarrow{LN}\small,\) выразим векторы \(\displaystyle \overrightarrow{LF}\) и \(\displaystyle \overrightarrow{DN}\) через стороны четырехугольника.
| \(\displaystyle \overrightarrow{LN}=\overrightarrow{LF}-\frac{\overrightarrow{DA}}{2}+\overrightarrow{DN}\small.\) | 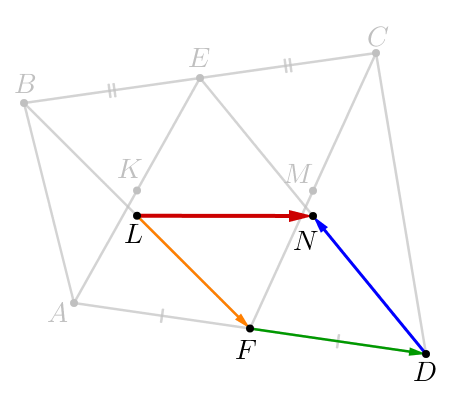 |
\(\displaystyle \overrightarrow{LF}=-\frac{\overrightarrow{AB}}{2}-\frac{\overrightarrow{DA}}{4}\small.\)
\(\displaystyle \overrightarrow{DN}=-\frac{\overrightarrow{CD}}{2}-\frac{\overrightarrow{BC}}{4}\small.\)
Тогда
\(\displaystyle \begin{aligned}\overrightarrow{LN}=\overrightarrow{LF}-\frac{\overrightarrow{DA}}{2}+\overrightarrow{DN}=-\frac{\overrightarrow{AB}}{2}-\frac{\overrightarrow{DA}}{4}-\frac{\overrightarrow{DA}}{2}-\frac{\overrightarrow{CD}}{2}-\frac{\overrightarrow{BC}}{4}=\\=-\frac{1}{2}\overrightarrow{AB}-\frac{1}{4}\overrightarrow{BC}-\frac{1}{2}\overrightarrow{CD}-\frac{3}{4}\overrightarrow{DA}\end{aligned}\small.\)
3. Чтобы сравнить векторы \(\displaystyle \overrightarrow{KM}\) и \(\displaystyle \overrightarrow{LN}\) рассмотрим их разность.
\(\displaystyle \overrightarrow{KM}-\overrightarrow{LN}=\)
\(\displaystyle \begin{aligned}=\left(\frac{1}{2}\overrightarrow{AB}+\frac{3}{4}\overrightarrow{BC}+\frac{1}{2}\overrightarrow{CD}+\frac{1}{4}\overrightarrow{DA}\right)-\left(-\frac{1}{2}\overrightarrow{AB}-\frac{1}{4}\overrightarrow{BC}-\frac{1}{2}\overrightarrow{CD}-\frac{3}{4}\overrightarrow{DA}\right)\\[10px]\end{aligned}\small.\)
Раскроем скобки:
\(\displaystyle \begin{aligned}\frac{1}{2}\overrightarrow{AB}+\frac{3}{4}\overrightarrow{BC}+\frac{1}{2}\overrightarrow{CD}+\frac{1}{4}\overrightarrow{DA}+\frac{1}{2}\overrightarrow{AB}+\frac{1}{4}\overrightarrow{BC}+\frac{1}{2}\overrightarrow{CD}+\frac{3}{4}\overrightarrow{DA}\small.\\[10px]\end{aligned}\)
Приведем подобные слагаемые и упростим результат:
\(\displaystyle \begin{aligned}\overrightarrow{AB}+\overrightarrow{BC}+\overrightarrow{CD}+\overrightarrow{DA}=\overrightarrow{AA}=0\small.\end{aligned}\)
Таким образом, видим, что разность векторов \(\displaystyle \overrightarrow{KM} \) и \(\displaystyle \overrightarrow{LN} \) равна нулю. Значит,
\(\displaystyle \overrightarrow{KM}=\overrightarrow{LN}\small.\)
Тогда отрезки \(\displaystyle KM\) и \(\displaystyle LN\) равны и параллельны. То есть \(\displaystyle KMNL\) – параллелограмм.