Найдите площадь \(\displaystyle S\) треугольника, если его периметр \(\displaystyle P\) равен \(\displaystyle 48{\small,}\) а радиус \(\displaystyle r\) вписанной окружности равен \(\displaystyle 3{\small.}\)
\(\displaystyle S=\)
Воспользуемся одной их формул для вычисления площади треугольника.
Площадь треугольника равна произведению его полупериметра на радиус вписанной в него окружности.
\(\displaystyle S_{\triangle}=p\cdot r{\small,}\) где \(\displaystyle p\) – полупериметр треугольника со сторонами \(\displaystyle \color{blue}{a}{\small,}\) \(\displaystyle \color{green}{b}{\small,}\) \(\displaystyle \color{magenta}{c}{\small:}\) \(\displaystyle p=\frac{\color{blue}{a}+\color{green}{b}+\color{magenta}{c}}{2}{\small;}\) \(\displaystyle \color{red}{r}\) – радиус вписанной окружности. | 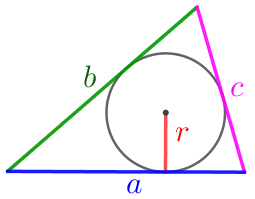 |
По условию периметр треугольника равен \(\displaystyle 48{\small.}\) Значит, полупериметр равен
\(\displaystyle p=\frac{1}{2}P=\frac{1}{2} \cdot 48=24{\small.}\)
Тогда
\(\displaystyle S=p\cdot r=24 \cdot 3=72{\small.}\)
Ответ: \(\displaystyle S=72{\small.}\)