В треугольник \(\displaystyle ABC\) вписана окружность радиуса \(\displaystyle 3{\small,}\) которая касается сторон \(\displaystyle AB{\small,}\) \(\displaystyle BC\) и \(\displaystyle CA\) в точках \(\displaystyle P{\small,}\) \(\displaystyle Q\) и \(\displaystyle R\) соответственно. Найдите площадь треугольника \(\displaystyle ABC{\small,}\) если \(\displaystyle AP=5{\small,}\) \(\displaystyle BQ=5{\small,}\) \(\displaystyle CR=6{\small.}\)
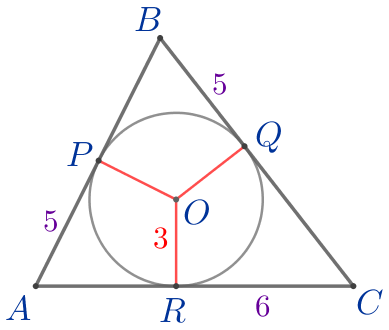
\(\displaystyle S_{\triangle ABC}=\)
Воспользуемся одной их формул для вычисления площади треугольника.
Площадь треугольника равна произведению его полупериметра на радиус вписанной в него окружности.
\(\displaystyle S_{\triangle}=p\cdot r{\small,}\) где \(\displaystyle p\) – полупериметр треугольника со сторонами \(\displaystyle \color{blue}{a}{\small,}\) \(\displaystyle \color{green}{b}{\small,}\) \(\displaystyle \color{magenta}{c}{\small:}\) \(\displaystyle p=\frac{\color{blue}{a}+\color{green}{b}+\color{magenta}{c}}{2}{\small;}\) \(\displaystyle \color{red}{r}\) – радиус вписанной окружности. | 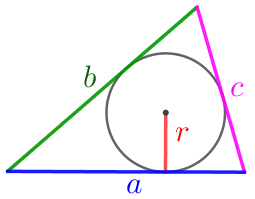 |
По условию радиус вписанной окружности равен \(\displaystyle 3{\small.}\) То есть
\(\displaystyle S_{\triangle ABC}=3 \cdot p{\small.}\)
Найдем полупериметр \(\displaystyle p\) треугольника\(\displaystyle ABC{\small.}\)
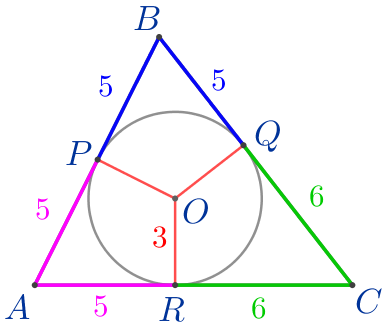 | Отрезки касательных, проведенных из одной точки к окружности, равны. Значит:
|
\(\displaystyle AB=10{\small;}\) \(\displaystyle BC=11{\small;}\) \(\displaystyle AC=11{\small.}\)
Периметр треугольника равен сумме длин всех его сторон:
\(\displaystyle P_{\triangle ABC}=AB+BC+AC=10+11+11=32{\small.}\)
Тогда
\(\displaystyle p=\frac{1}{2} \cdot P=\frac{1}{2} \cdot 32=16{\small.}\)
В результате получаем:
\(\displaystyle S_{\triangle ABC}=3 \cdot p=3 \cdot 16=48{\small.}\)
Ответ: \(\displaystyle S_{\triangle ABC}=48{\small.}\)