Задание
В треугольнике \(\displaystyle ABC\) угол \(\displaystyle C\) равен \(\displaystyle 90^{\circ} {\small,}\) \(\displaystyle BC=10 {\small,}\) \(\displaystyle AC=7{\small.}\) Найдите \(\displaystyle \tg \angle B {\small.}\)
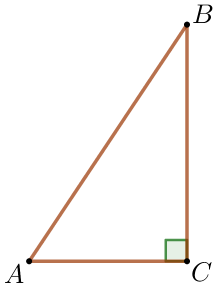
Решение
В прямоугольном треугольнике тангенс острого угла равен отношению противолежащего катета к прилежащему катету. Значит,
\(\displaystyle \tg \angle B= \frac{AC}{BC}{\small.}\)
По условию \(\displaystyle AC=7{\small,}\) \(\displaystyle BC=10{\small.}\) Тогда
\(\displaystyle \tg \angle B= \frac{7}{10}=0{,}7{\small.}\)
Ответ: \(\displaystyle 0{,}7{\small.}\)