Дана система линейных уравнений
\(\displaystyle \begin{cases}{{10}}y-{\dfrac{5}{4}}x=9{,}2(\,y+0{,}3x\,)-2{,}7+{\dfrac{x}{7}}{\small , }\\[10px]{\dfrac{5x}{8}}+3{,}4-6{,}2y=4{,}5(\,1{,}7x-{\dfrac{y}{3}}\,)+{\dfrac{7}{20}}\end{cases}\)
и графики двух линейных функций:
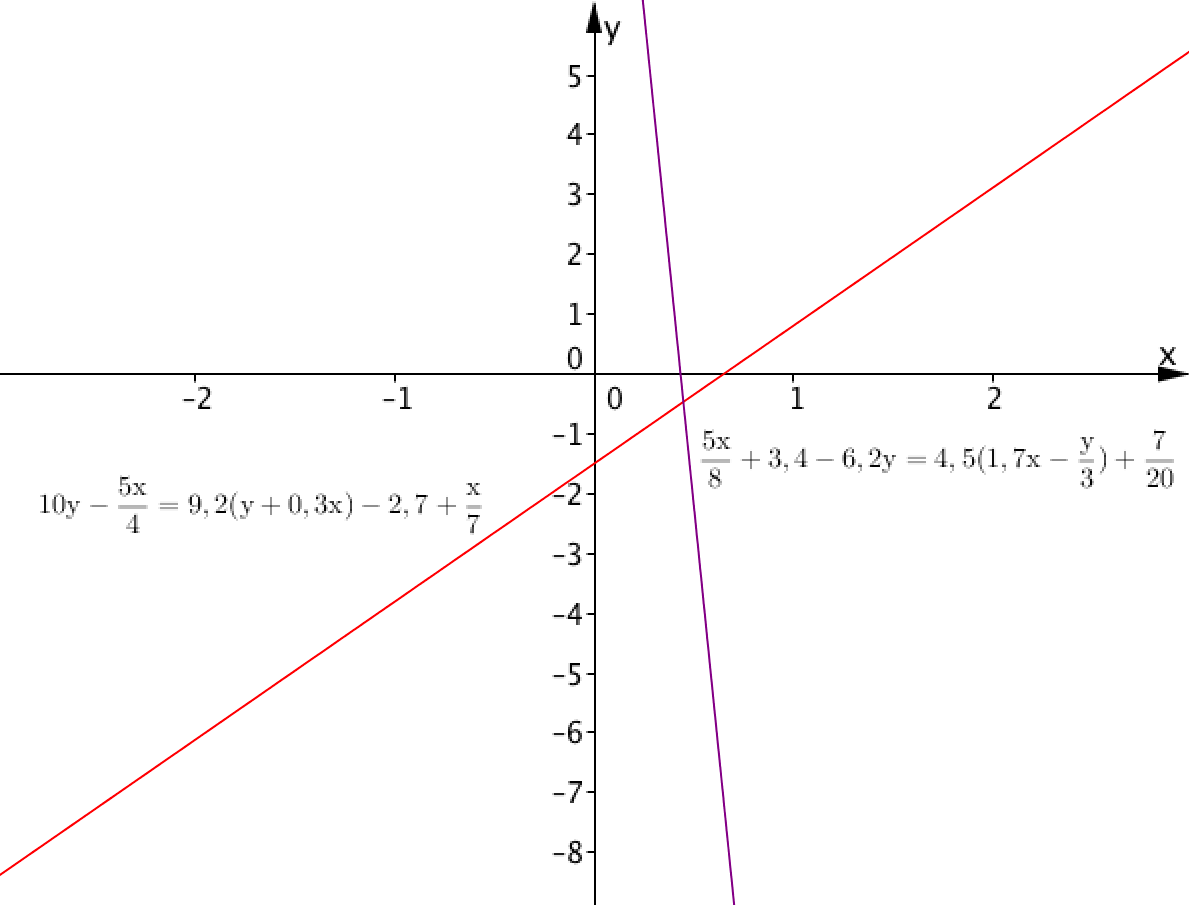
Определите число решений системы линейных уравнений.
Нам дана система линейных уравнений
\(\displaystyle \begin{cases}{{10}}y-{\dfrac{5}{4}}x=9{,}2(\,y+0{,}3x\,)-2{,}7+{\dfrac{x}{7}}{\small , }\\[10px]{\dfrac{5x}{8}}+3{,}4-6{,}2y=4{,}5(\,1{,}7x-{\dfrac{y}{3}}\,)+{\dfrac{7}{20}}\end{cases}\)
Мы знаем, что каждому линейному уравнению на координатной плоскости соответствует прямая.
Возможны три случая:
1) прямые, соответствующие уравнениям, пересекаются в одной точке, тогда система имеет единственное решение;
2) прямые, соответствующие уравнениям, не пересекаются (параллельны), тогда система не имеет решений;
3) прямые, соответствующие уравнениям, совпадают, тогда система имеет бесконечно много решений.
Ответ: одно решение.