Задание
Укажите верную цепочку включений:
Решение
Замечание / комментарий
Числа \(\displaystyle 1{\small,}\) \(\displaystyle 2{\small,}\) \(\displaystyle 3 {\small,} \dots {\small,} \) которые используют при счёте, называют натуральными. Они составляют множество натуральных чисел.
Натуральные числа, противоположные им числа и число нуль образуют множество целых чисел.
Целые и дробные числа составляют множество рациональных чисел.
Информация
Общеприняты следующие обозначения:
- \(\displaystyle N\) – множество натуральных чисел ( от первой буквы латинского слова naturalis – естественный),
- \(\displaystyle Z\) – множество целых чисел ( от первой буквы немецкого слова Zahl – число),
- \(\displaystyle Q\) – множество рациональных чисел ( от первой буквы французского слова quolient – число).
Множество натуральных чисел является подмножеством множества целых чисел: \(\displaystyle N \subset Z {\small.}\)
Множество целых чисел является подмножеством множества рациональных чисел: \(\displaystyle Z \subset Q {\small.}\)
| \(\displaystyle N \subset Z \subset Q \) |  |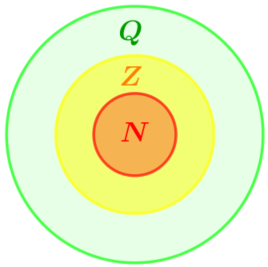
Ответ: \(\displaystyle N \subset Z \subset Q {\small.}\)