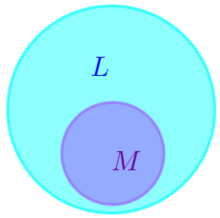
Какое из множеств \(\displaystyle (A\) или \(\displaystyle B) \) является подмножеством другого, если
\(\displaystyle A\) – множество правильных треугольников,
\(\displaystyle B\) – множество равнобедренных треугольников.
Множество
| Правильный треугольник – это треугольник, у которого все стороны равны между собой по длине. | 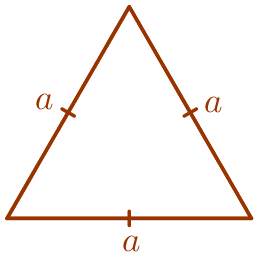 |
| Равнобедренный треугольник – это треугольник, у которого две стороны равны между собой по длине. | 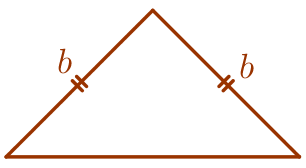 |
Любой правильный треугольник является равнобедренным, но не любой равнобедренный треугольник является правильным.
То есть каждый элемент из множества \(\displaystyle A\) является элементом множества \(\displaystyle B{\small.}\)
Ответ: Множество \(\displaystyle A\) является подмножеством множества \(\displaystyle B{\small.}\)