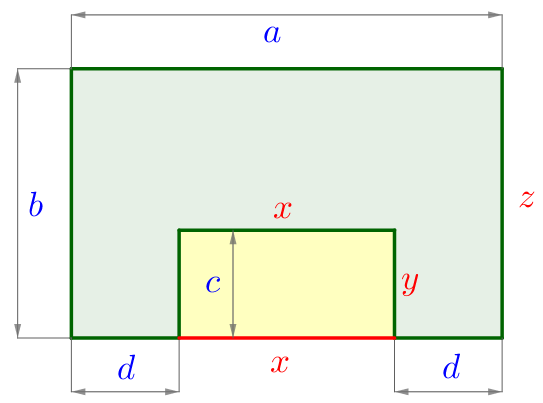
На рисунке изображена фигура (все углы прямые). Длины отрезков указаны в сантиметрах.
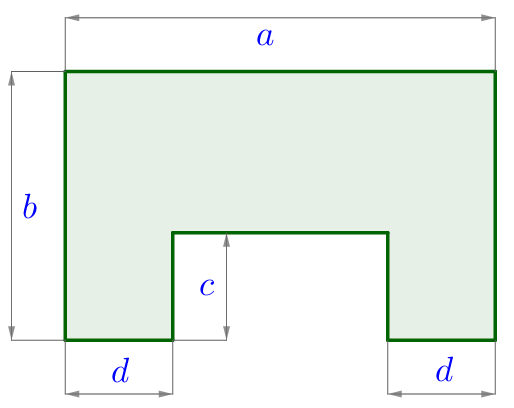
Периметр данной фигуры можно вычислить по формуле
Периметр многоугольника равен сумме длин всех его сторон.
Составим формулу для вычисления периметра данной фигуры.
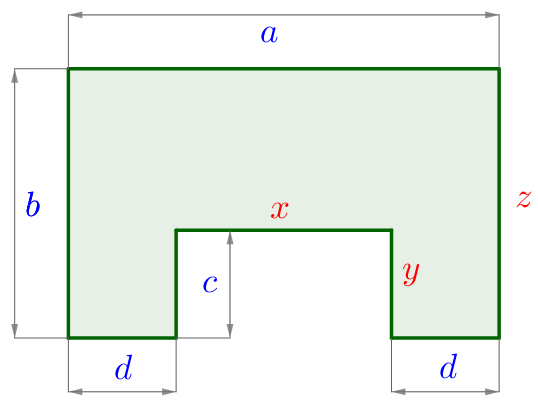 | На исходном рисунке указаны длины пяти сторон \(\displaystyle a{\small,}\) \(\displaystyle b{\small,}\) \(\displaystyle d{\small,}\) \(\displaystyle c{\small,}\) \(\displaystyle d\) данного восьмиугольника. Пусть \(\displaystyle x{\small,}\) \(\displaystyle y\) и \(\displaystyle z\) – длины оставшихся трёх сторон. Тогда периметр \(\displaystyle P\) восьмиугольника равен \(\displaystyle P=a+b+d+c+x+y+d+z{\small.}\) |
Выполним дополнительное построение как показано на рисунке:
| Так как все углы прямые, то в результате построения получили пару прямоугольников \(\displaystyle (\)большой зелёный и маленький жёлтый\(\displaystyle ){\small.}\) В прямоугольнике противоположные стороны равны. Значит, \(\displaystyle y=c{\small,}\) \(\displaystyle z=b{\small,}\) \(\displaystyle d+x+d=a{\small.}\) |
Из равенства \(\displaystyle d+x+d=a\) выразим \(\displaystyle x{\small:}\) \(\displaystyle x+2d=a{\small,}\) \(\displaystyle x=a-2d{\small.}\) Тогда периметр \(\displaystyle P\) восьмиугольника равен: \(\displaystyle\begin{aligned}P&=a+b+d+c+\color{red}{x}+\color{darkviolet}{y}+d+\color{magenta}{z}=\\&=a+b+d+c+\color{red}{a-2d}+\color{darkviolet}{c}+d+\color{magenta}{b}=\\&=\color{orange}{\underline{\color{black}{a}}}+\color{orange}{\underline{\underline{\color{black}{b}}}}+\cancel{d}+\color{orange}{\underline{\underline{\underline{\color{black}{c}}}}}+\color{orange}{\underline{\color{black}{a}}}-\cancel{2d}+\color{orange}{\underline{\underline{\underline{\color{black}{c}}}}}+\cancel{d}+\color{orange}{\underline{\underline{\color{black}{b}}}}=\\&\kern{5em}=2a+2b+2c{\small.}\end{aligned}\) | 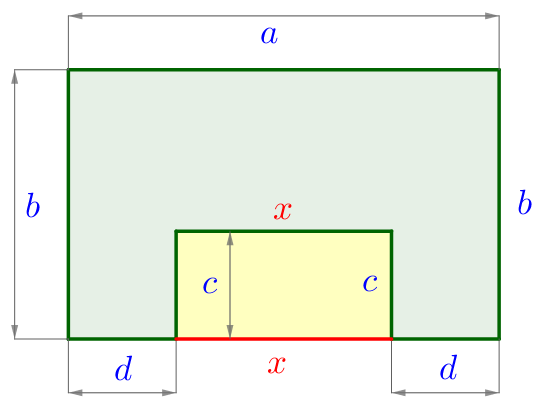 |
То есть периметр данной фигуры можно вычислить по формуле \(\displaystyle 2a+2b+2c{\small.}\)
Ответ: \(\displaystyle 2a+2b+2c{\small.}\)