Ребро куба равно \(\displaystyle a\ {\scriptsize м.}\)
От этого куба отрезан прямоугольный параллелепипед, высота которого равна\(\displaystyle h\ {\scriptsize м.}\)
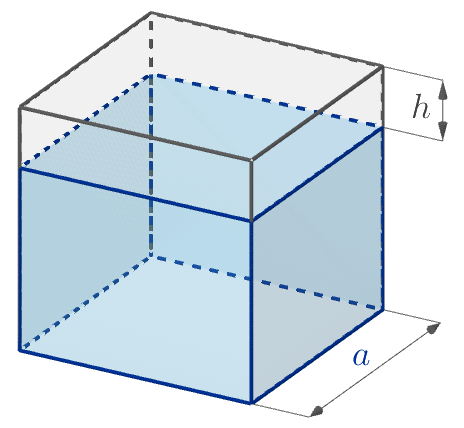
Объём оставшейся части можно посчитать по формуле
Воспользуемся правилом.
Объем прямоугольного параллелепипеда
Объем прямоугольного параллелепипеда \(\displaystyle V \) равен произведению трех его измерений:
\(\displaystyle V=abc{ \small ,} \)
где \(\displaystyle a { \small ,}\,b{ \small ,}\,c\) – измерения прямоугольного параллелепипеда (длины трех ребер, имеющих общую вершину).
\(\displaystyle \color{red}{ 1)} \) Найдем объём \(\displaystyle V_1\) исходного куба.
Все ребра куба равны \(\displaystyle a{\small.}\) Значит, объем куба равен
\(\displaystyle V_1=a\cdot a \cdot a =a^3{\small.}\)
\(\displaystyle \color{red}{ 2)} \) Найдем объём \(\displaystyle V_2\) отрезанного параллелепипеда.
Определим по рисунку измерения отрезанного прямоугольного параллелепипеда:
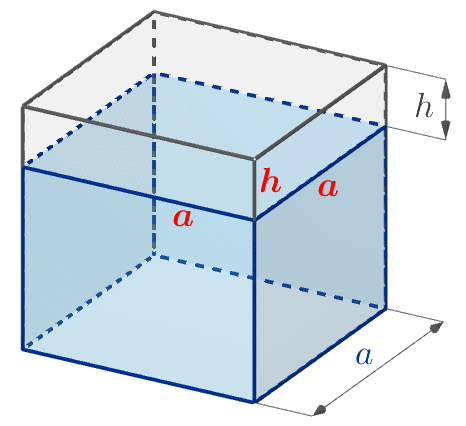 | Длины трёх рёбер, имеющих общую вершину, равны \(\displaystyle \color{red}{a}{\small,}\) \(\displaystyle \color{red}{a}\) и \(\displaystyle \color{red}{h}{\small.}\) Значит, объём \(\displaystyle V_2\) отрезанного прямоугольного параллелепипеда можно вычислить по формуле: \(\displaystyle V_2=a \cdot a\cdot h=a^2h{\small.}\) |
\(\displaystyle \color{red}{ 3)} \) Найдем объём \(\displaystyle V\) оставшейся части.
Из объёма исходного куба вычтем объём отрезанного параллелепипеда:
\(\displaystyle V=V_1-V_2{\small,}\)
\(\displaystyle V=a^3-a^2h{\small.}\)
Ответ: \(\displaystyle a^3-a^2h{\small.}\)