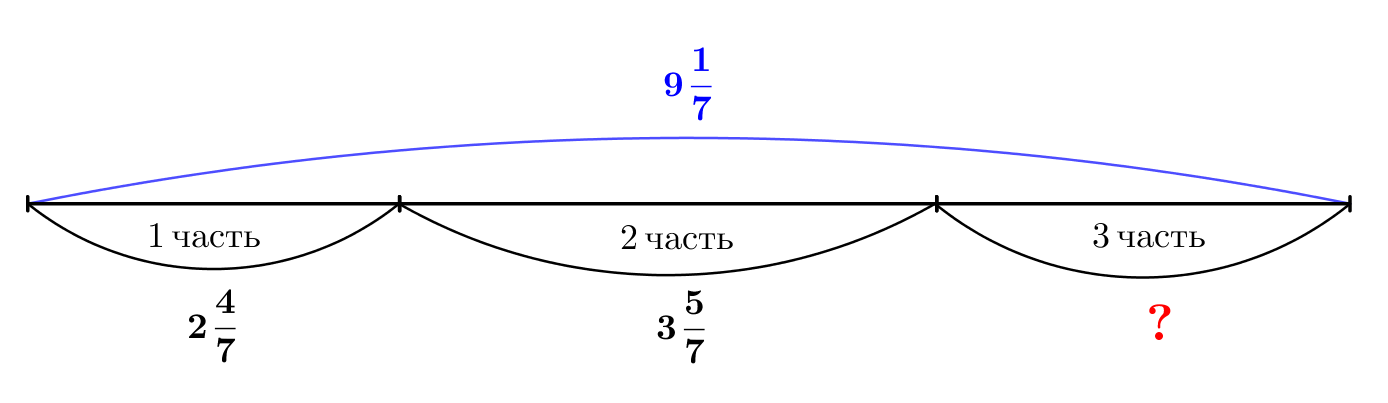
Веревку длиной \(\displaystyle 9\frac{1}{7}\)м разделили на три части. Длина первой части равна \(\displaystyle 2\frac{4}{7}\)м, длина второй – \(\displaystyle 3\frac{5}{7}\)м.
А чему равна длина третьей части?
Схематично изобразим условие задачи:
Решение 1.
Чтобы найти длину третьей части, нужно:
- найти сумму длин \(\displaystyle 1\) и \(\displaystyle 2\) частей,
- из всей длины веревки вычесть эту сумму.
\(\displaystyle 2\frac{4}{7}+3\frac{5}{7}=6\frac{2}{7}\)м.
\(\displaystyle 9\frac{1}{7}-6\frac{2}{7}=2\frac{6}{7}\)м.
Ответ: \(\displaystyle 2\frac{6}{7}\)м.
Решение 2.
Длина всей веревки \(\displaystyle 9\frac{1}{7}\) м, длина первой части равна \(\displaystyle 2\frac{4}{7}\) м, длина второй – \(\displaystyle 3\frac{5}{7}\) м.
Тогда длина оставшейся третьей части равна
\(\displaystyle 9\frac{1}{7}-2\frac{4}{7}-3\frac{5}{7}\)м.
Найдем значение данного выражения. Для этого
- переведем смешанные числа в неправильные дроби,
- выполним вычитание неправильных дробей.
Переводим смешанные числа в неправильные дроби:
\(\displaystyle \begin{aligned}\\\color{blue}{9\frac{1}{7}}=\frac{9\cdot7+1}{7}=\color{blue}{\frac{64}{7}}\small,\\[15px]\color{green}{2\frac{4}{7}}=\frac{2\cdot7+4}{7}=\color{green}{\frac{18}{7}}\small,\\[15px]\color{purple}{3\frac{5}{7}}=\frac{3\cdot7+5}{7}=\color{purple}{\frac{26}{7}}\small.\\\end{aligned}\)
Выполняем вычитание неправильных дробей с одинаковыми знаменателями:
\(\displaystyle \color{blue}{\frac{64}{7}}-\color{green}{\frac{18}{7}}-\color{purple}{\frac{26}{7}}=\frac{\color{blue}{64}-\color{green}{18}-\color{purple}{26}}{7}=\frac{20}{7}\small.\)
Выделим целую часть:
\(\displaystyle \frac{20}{7}=\frac{2\cdot7+6}{7}=2\frac{6}{7}\small.\)
Ответ: \(\displaystyle 2\frac{6}{7}\)м.