На рисунке изображён график функции \(\displaystyle y=f\left(x\right){\small .}\) Числа \(\displaystyle a {\small ,} \,b {\small ,} \,c {\small ,} \, d\) и \(\displaystyle e\) задают на оси \(\displaystyle Ox\) интервалы. Пользуясь графиком, поставьте в соответствие каждому интервалу характеристику функции.
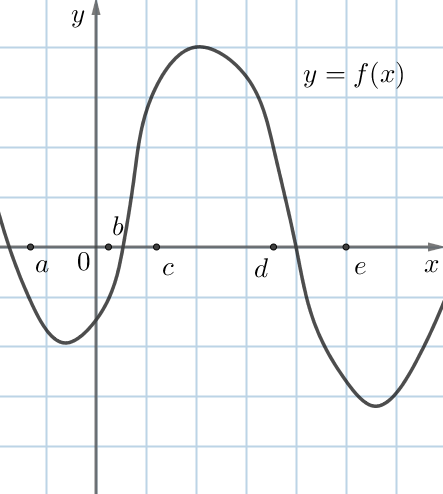
| ИНТЕРВАЛЫ | ХАРАКТЕРИСТИКИ |
| \(\displaystyle А)\) \(\displaystyle (a{\small ,}\, b)\) | \(\displaystyle 1)\) значения функции положительны в каждой точке интервала |
| \(\displaystyle Б)\) \(\displaystyle (b{\small ,} \, c)\) | \(\displaystyle 2)\) функция убывает на интервале |
| \(\displaystyle В)\) \(\displaystyle (c{\small ,} \,d)\) | \(\displaystyle 3)\) значения функции отрицательны в каждой точке интервала |
| \(\displaystyle Г)\) \(\displaystyle (d{\small ,}\, e)\) | \(\displaystyle 4)\) функция возрастает на интервале |
В таблице под каждой буквой укажите соответствующий номер.
| \(\displaystyle A\) | \(\displaystyle Б\) | \(\displaystyle В\) | \(\displaystyle Г\) |
Даны четыре интервала на оси \(\displaystyle Ox\) и четыре характеристики функции.
- Характеристики \(\displaystyle 1)\) и \(\displaystyle 3){\small }\) касаются значений функции (положительны / отрицательны).
- Характеристики \(\displaystyle 2)\) и \(\displaystyle 4){\small }\) касаются поведения функции (убывание / возрастание).
Требуется определить, какая характеристика соответствует каждому интервалу.
Для удобства выделим интервалы цветом.
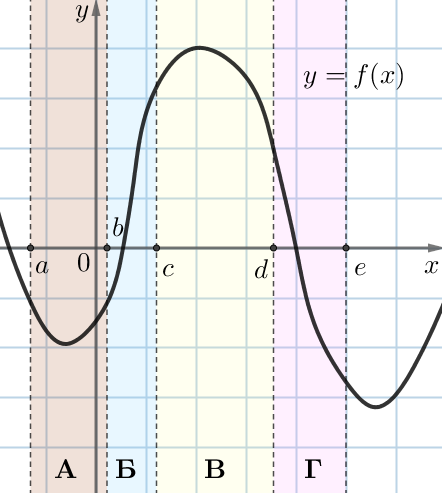
1. Сначала определим, каким интервалам соответствуют характеристики \(\displaystyle 1)\) и \(\displaystyle 3){\small .}\)
\(\displaystyle 3)\) Значения функции отрицательны в каждой точке интервала \(\displaystyle А{\small .}\)
Положительные значения функции соответствуют участкам графика, расположенным выше оси \(\displaystyle Ox{\small .}\)
Отрицательные значения функции соответствуют участкам графика, расположенным ниже оси \(\displaystyle Ox{\small .}\)
Рассмотрим последовательно все интервалы, начиная с \(\displaystyle А{\small .}\)
Выберем те интервалы, для которых график лежит или только выше, или только ниже оси \(\displaystyle Ox{\small .}\)
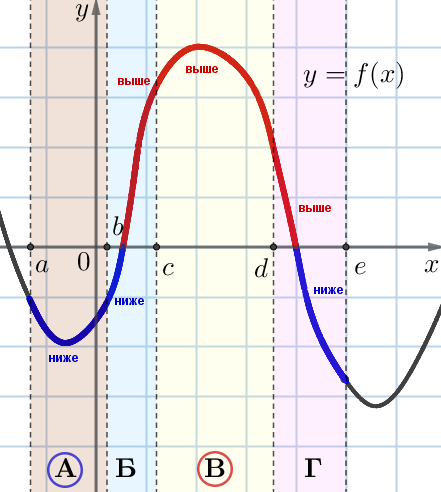
Видим:
- только для всех точек интервала \(\displaystyle А\) график лежит ниже оси \(\displaystyle Ox{\small ,}\) значит, функция принимает на этом интервале отрицательные значения;
- только для всех точек интервала \(\displaystyle В\) график лежит выше оси \(\displaystyle Ox{\small ,}\) значит, функция принимает на этом интервале положительные значения.
Будем постепенно заполнять таблицу.
| \(\displaystyle А\) | \(\displaystyle Б\) | \(\displaystyle В\) | \(\displaystyle Г\) |
| \(\displaystyle 3\) | \(\displaystyle 1\) |
2. Определим, каким интервалам соответствуют оставшиеся характеристики \(\displaystyle 2)\) и \(\displaystyle 4){\small .}\)
\(\displaystyle 4)\) Функция возрастает на интервале \(\displaystyle Б{\small .}\)
Рассмотрим последовательно все интервалы, начиная с \(\displaystyle А{\small .}\)
На каждом из интервалов отметим промежутки возрастания и убывания функции. Выберем те интервалы, на которых функция убывает (возрастает).
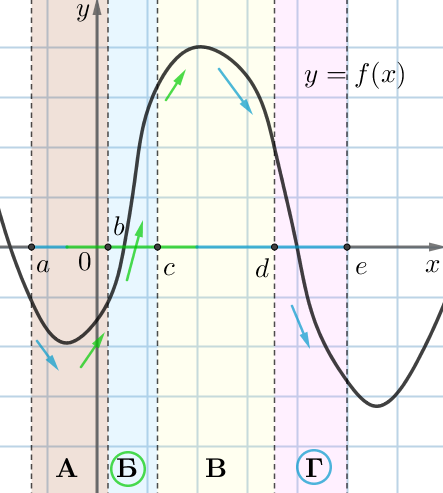
Видим:
- только на интервале \(\displaystyle Б{\small }\) функция возрастает;
- только на интервале \(\displaystyle Г\) функция убывает.
Тогда окончательно получаем:
| \(\displaystyle А\) | \(\displaystyle Б\) | \(\displaystyle В\) | \(\displaystyle Г\) |
| \(\displaystyle 3\) | \(\displaystyle 4\) | \(\displaystyle 1\) | \(\displaystyle 2\) |