Функция \(\displaystyle y=f(x)\) задана на отрезке \(\displaystyle [-5;\,6]\) с помощью графика:
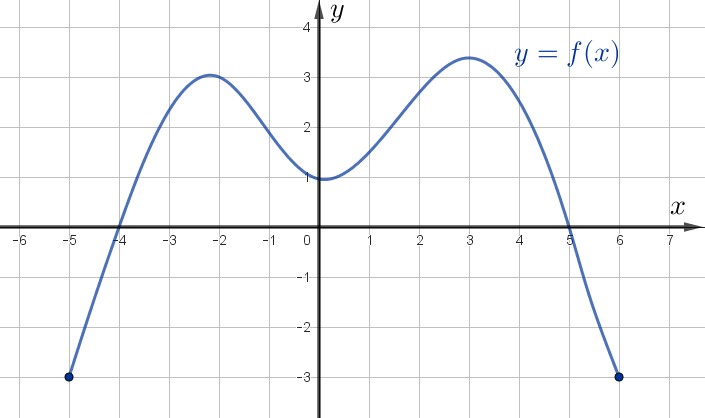
Найдите промежутки знакопостоянства функции. Если промежутков несколько, разделяйте их точкой с запятой.
\(\displaystyle f(x)>0\) при каждом \(\displaystyle x\) из
\(\displaystyle f(x)<0\) при каждом \(\displaystyle x\) из
Положительные значения функции соответствуют точкам графика, ординаты (координаты \(\displaystyle y\)) которых больше нуля.
То есть это все точки графика, лежащие выше оси \(\displaystyle Ox\small.\)
Отметим их на графике.
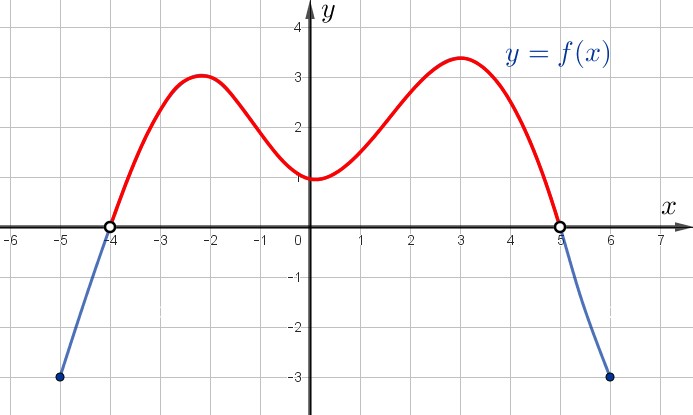
Выясним, где на оси \(\displaystyle Ox\) располагаются абсциссы (координаты \(\displaystyle x\)) данных точек.
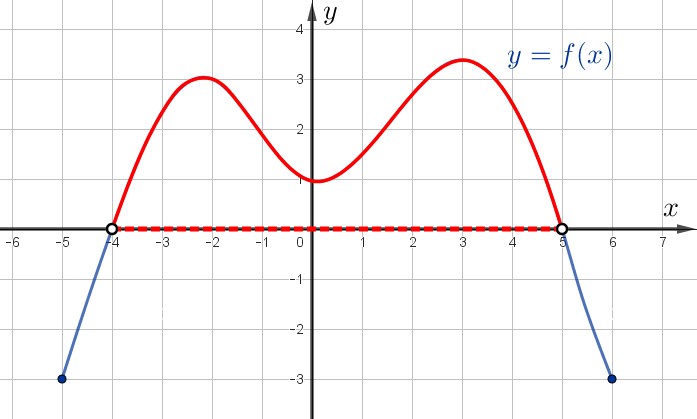
Видим, что это все точки между \(\displaystyle -4\) и \(\displaystyle 5 {\small .}\)
То есть функция принимает положительные значения на промежутке \(\displaystyle \color {red}{(-4;\,5)} \small.\)
Отрицательные значения функции соответствуют точкам графика, ординаты (координаты \(\displaystyle y\)) которых меньше нуля.
То есть это все точки графика, лежащие ниже оси \(\displaystyle Ox\small.\)
Отметим их на графике.
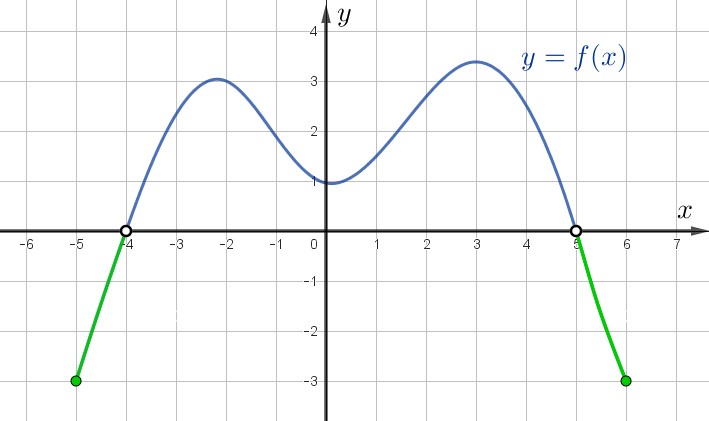
Выясним, где на оси \(\displaystyle Ox\) располагаются абсциссы (координаты \(\displaystyle x\)) данных точек.
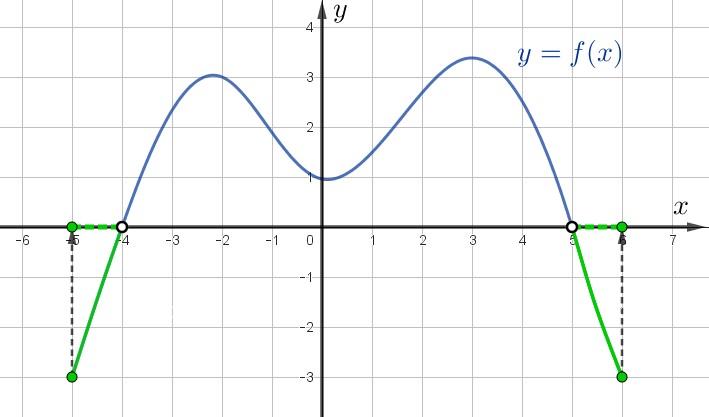
Видим, что это:
- все точки между \(\displaystyle -5\) и \(\displaystyle -4 {\small ,}\) включая \(\displaystyle -5\) и не включая \(\displaystyle -4 {\small ;}\)
- все точки между \(\displaystyle 5\) и \(\displaystyle 6 {\small ,}\) не включая \(\displaystyle 5\) и включая \(\displaystyle 6 {\small .}\)
То есть функция принимает отрицательные значения на промежутках
\(\displaystyle \color {#00cc00}{[-5;\,-4)}\) и \(\displaystyle \color{#00cc00}{(5;\,6]}\small.\)
Получили ответ:
| \(\displaystyle f(x)>0\) | при \(\displaystyle x \in {(-4;\,5)} \small.\) |
| \(\displaystyle f(x)<0\) | при \(\displaystyle x \in [-5;\,-4 ) ; (5;\,6] {\small.}\) |