В ромбе \(\displaystyle ABCD\) угол между диагональю \(\displaystyle AC\) и стороной \(\displaystyle AB\) равен \(\displaystyle 35^{\circ}{\small.}\) Найдите острый угол ромба. Ответ дайте в градусах.
\(\displaystyle ^{\circ}\)
Требуется найти острый угол данного ромба. | 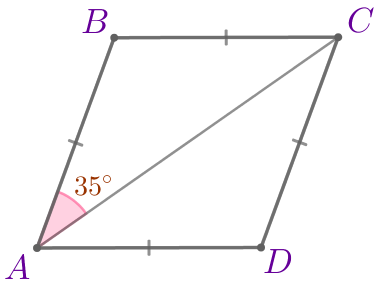 |
| Диагонали ромба являются биссектрисами его углов. | 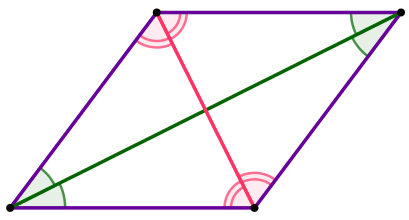 |
По свойству ромба диагональ \(\displaystyle AC\) делит угол \(\displaystyle A\) пополам, значит, \(\displaystyle \angle A=2 \cdot \angle BAC=2 \cdot 35^{\circ}=70^{\circ}{\small.} \) | 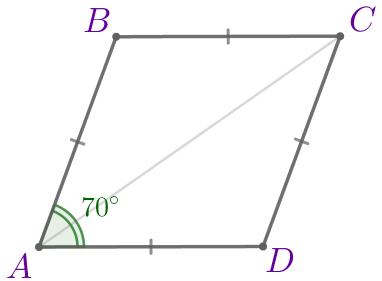 |
Поскольку \(\displaystyle 70^{\circ}<90^{\circ}{\small,}\) то \(\displaystyle \angle A\) – это острый угол ромба и он равен \(\displaystyle 70^{\circ}{\small.}\)
Ответ: \(\displaystyle 70^\circ {\small .}\)