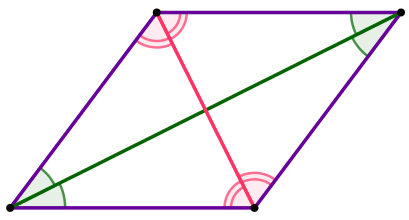
В ромбе \(\displaystyle ABCD\) угол \(\displaystyle B\) равен \(\displaystyle 80^{\circ}{\small.}\) Найдите угол между стороной \(\displaystyle CD\) и диагональю \(\displaystyle AC{\small.}\)
\(\displaystyle ^{\circ}\)
| Ромбом называется параллелограмм, у которого все стороны равны. | 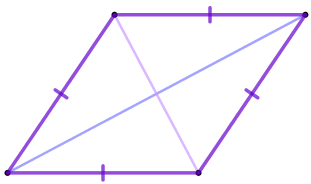 |
Требуется найти угол \(\displaystyle ACD{\small.}\) | 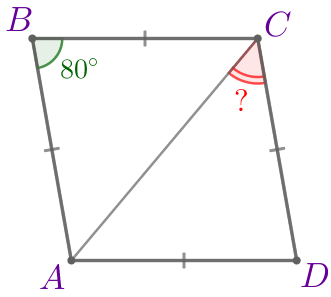 |
Поскольку ромб – это параллелограмм, то все свойства параллелограмма верны для ромба.
Так как в параллелограмме сумма углов, прилежащих к одной стороне, равна \(\displaystyle 180^{\circ}{ \small ,}\) то \(\displaystyle \angle B+ \angle C=180^{\circ}{\small;}\) \(\displaystyle \angle C=180^{\circ}- \angle B=180^{\circ}-80^{\circ} =100^{\circ}{\small.}\) | 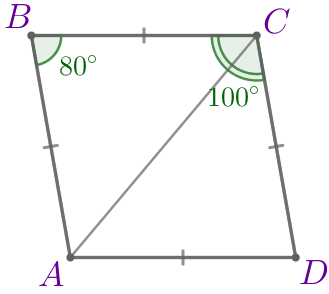 |
\(\displaystyle \angle ACD=\angle BCA=\frac{\angle C}{2}=\frac{100^{\circ}}{2}=50^{\circ}{\small.} \) | 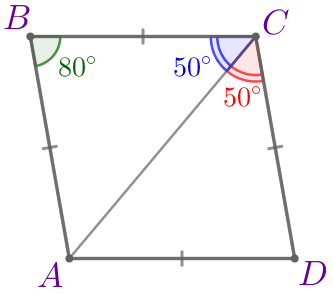 |
Угол между стороной \(\displaystyle CD\) и диагональю \(\displaystyle AC\) равен \(\displaystyle 50^{\circ}{\small.} \)
Ответ: \(\displaystyle 50^{\circ}{\small.} \)