Skip to main content

Теория: Свойства

Задание

Внутри квадрата \(\displaystyle ABCD\) взята точка \(\displaystyle K\) и на отрезке \(\displaystyle AK\) как на стороне построен квадрат \(\displaystyle AKLM{\small,}\) у которого сторона \(\displaystyle KL\) пересекает сторону \(\displaystyle AD{\small.}\) Найдите длину отрезка \(\displaystyle DM{\small,}\) если \(\displaystyle AB=7{\small,}\) \(\displaystyle AK=6{\small,}\) \(\displaystyle BK=7{,}7{\small.}\)

\(\displaystyle DM=\) 

Решение

Определение

Квадратом называется параллелограмм, у которого все стороны равны и все углы прямые.

  • \(\displaystyle ABCD\) – квадрат;
  • \(\displaystyle AB=7{\small;}\)
  • точка \(\displaystyle K\) лежит внутри квадрата \(\displaystyle ABCD{\small;}\)
  • \(\displaystyle AK=6{\small;}\)
  • \(\displaystyle BK=7{,}7{\small;}\)
  • \(\displaystyle AKLM\) – квадрат;
  • \(\displaystyle KL\) пересекает \(\displaystyle AD{\small.}\)

 

Требуется найти длину отрезка \(\displaystyle DM{\small.}\)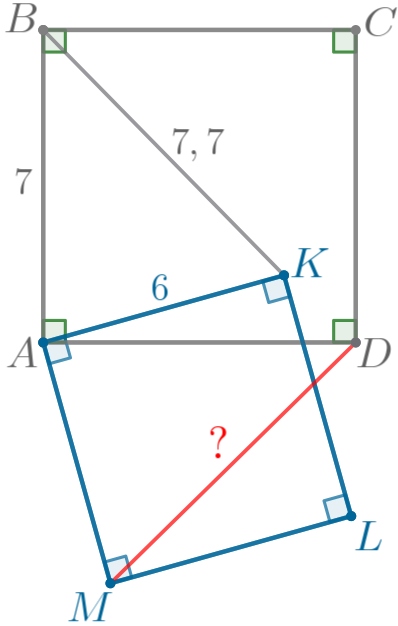

 

Рассмотрим треугольники \(\displaystyle ABK\) и \(\displaystyle ADM{\small.}\)

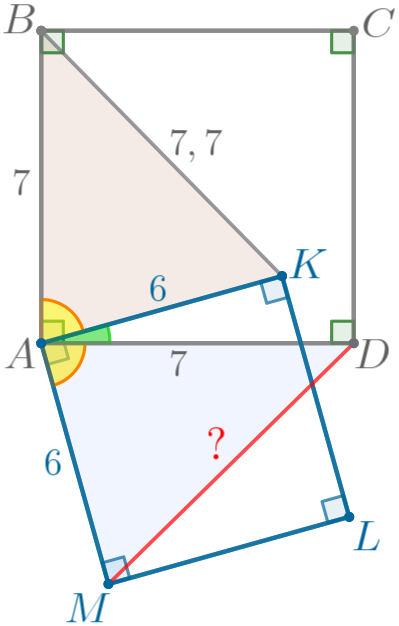\(\displaystyle AB=AD=7\) – стороны квадрата \(\displaystyle ABCD{\small;}\)

\(\displaystyle AK=AM=6\) – стороны квадрата \(\displaystyle AKLM{\small;}\)

\(\displaystyle \angle BAK=\angle DAM{\small.}\)

Следовательно,

\(\displaystyle \triangle ABK=\triangle ADM\)

по двум сторонам и углу между ними.

Значит, 

\(\displaystyle DM=BK=7{,}7{\small.}\)

Ответ: \(\displaystyle DM=7{,}7{\small.}\)