На сторонах \(\displaystyle AD\) и \(\displaystyle CD\) квадрата \(\displaystyle ABCD\) отметили соответственно точки \(\displaystyle K\) и \(\displaystyle L\) так, что \(\displaystyle BK \perp AL{\small.}\) Найдите длину отрезка \(\displaystyle AL{\small,}\) если \(\displaystyle AB=7{\small,}\) \(\displaystyle BK=8{\small.}\)
\(\displaystyle AL=\)
Выполним построение по условию задачи.
| 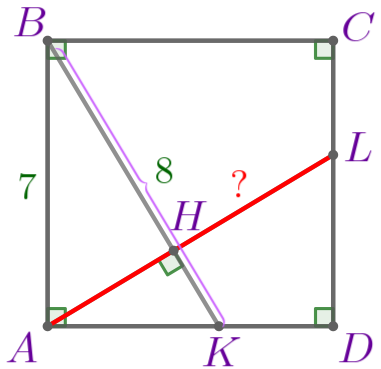 |
Требуется найти длину отрезка \(\displaystyle AL{\small.}\)
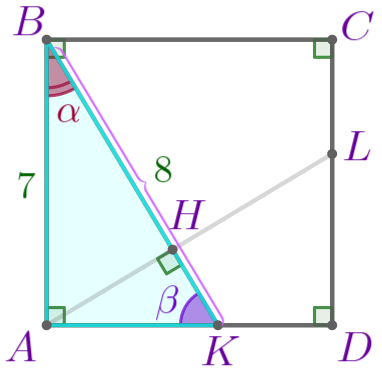 | В прямоугольном треугольнике сумма острых углов равна \(\displaystyle 90^{\circ}{\small.}\) Значит, \(\displaystyle \angle ABK+ \angle AKB= 90^{\circ}{\small.}\) Обозначим \(\displaystyle \color{darkred}{\alpha}=\angle ABK{\small,}\) \(\displaystyle \color{darkviolet}{\beta}=\angle AKB{\small.}\) То есть \(\displaystyle \color{darkred}{\alpha}+\color{darkviolet}{\beta}=90^{\circ}{\small.}\) |
 | Запишем сумму острых углов прямоугольного треугольника: \(\displaystyle \angle HAK+ \angle HKA= 90^{\circ}{\small.}\) Подставим \(\displaystyle \angle HKA=\color{darkviolet}{\beta}{\small:}\) \(\displaystyle \angle HAK+ \color{darkviolet}{\beta}= 90^{\circ}{\small.}\) Значит, \(\displaystyle \angle HAK= 90^{\circ}-\color{darkviolet}{\beta}=\color{darkred}{\alpha}{\small.}\) |
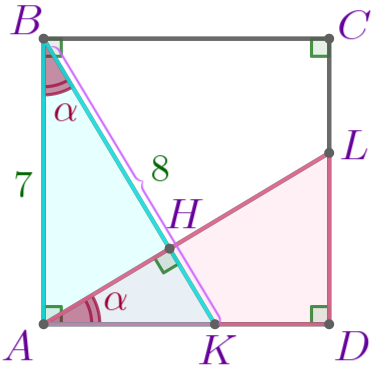 |
Следовательно, \(\displaystyle \triangle DAL= \triangle ABK\) – по катету и острому углу. Значит, \(\displaystyle AL=BK=8{\small.}\) |
Ответ: \(\displaystyle AL=8{\small.}\)