Диагональ \(\displaystyle FC\) квадрата \(\displaystyle FECD\) равна \(\displaystyle 6\, \footnotesize см{\small.}\) Прямая, проходящая через точку \(\displaystyle F\) и перепендикулярная к прямой \(\displaystyle FC{\small,}\) пересекает прямые \(\displaystyle EC\) и \(\displaystyle CD\) соответственно в точках \(\displaystyle M\) и \(\displaystyle N{\small.}\) Найдите \(\displaystyle MN{\small.}\)
\(\displaystyle MN=\) \(\displaystyle \, \footnotesize см{\small.}\)
По условию задачи выполним построение.
Требуется найти длину отрезка \(\displaystyle MN{\small.}\) | 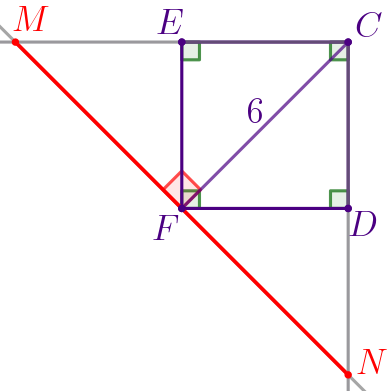 |
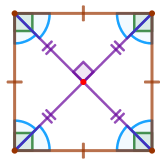 | \(\displaystyle 1.\) Все углы квадрата прямые. \(\displaystyle 2.\) Диагонали квадрата равны, взаимно перпендикулярны, точкой пересечения делятся пополам и делят углы квадрата пополам. |
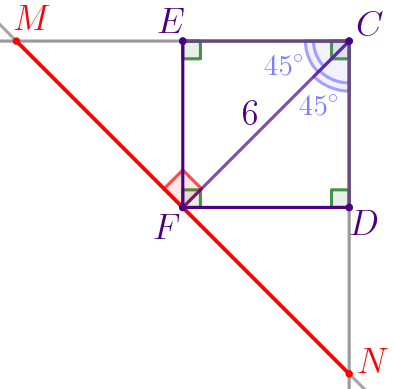 | По свойству квадрата диагональ \(\displaystyle FC\) делит угол \(\displaystyle C\) квадрата \(\displaystyle FECD\) пополам. То есть
\(\displaystyle \angle ECA= \angle DCF=90^{\circ}:2=45^{\circ}{\small.}\) |
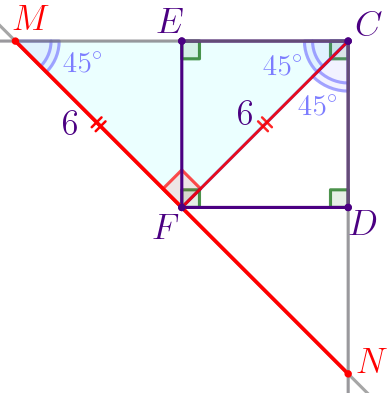 | Сумма острых углов прямоугольного треугольника равна \(\displaystyle 90^{\circ}{\small.}\) Тогда \(\displaystyle \angle FMC= 90^{\circ}-\angle FCM=90^{\circ}-45^{\circ}=45^{\circ}{\small.}\) Значит, \(\displaystyle \angle FMC= \angle FCM{\small.}\) Следовательно, \(\displaystyle \triangle FMC\) – равнобедренный, то есть \(\displaystyle FM=FC=6\, \footnotesize см{\small.}\) |
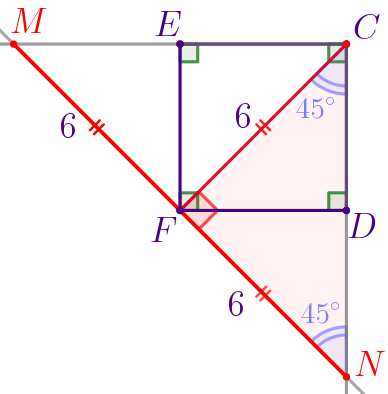 | Сумма острых углов прямоугольного треугольника равна \(\displaystyle 90^{\circ}{\small.}\) Тогда \(\displaystyle \angle FNC= 90^{\circ}-\angle FCN=90^{\circ}-45^{\circ}=45^{\circ}{\small.}\) Значит, \(\displaystyle \angle FNC= \angle FCN{\small.}\) Следовательно, \(\displaystyle \triangle FNC\) – равнобедренный, то есть \(\displaystyle FN=FC=6\, \footnotesize см{\small.}\) |
Так как точка \(\displaystyle F\) лежит на отрезке \(\displaystyle MN{\small,}\) то
\(\displaystyle MN=FM+FN=6+6=12\, \footnotesize см{\small.}\)
Ответ: \(\displaystyle MN=12\, \footnotesize см{\small.}\)