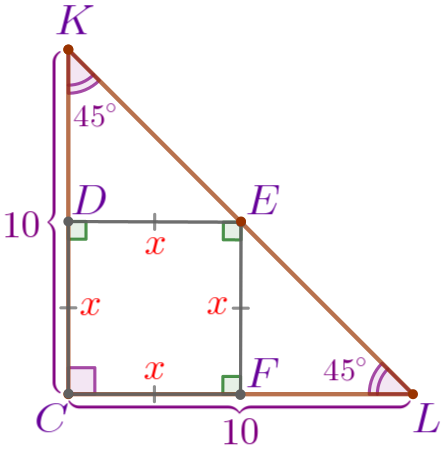
Даны равнобедренный прямоугольный треугольник \(\displaystyle KLC\) с прямым углом \(\displaystyle C{\small,}\) катетом \(\displaystyle KC=10\, \footnotesize см\) и квадрат \(\displaystyle CDEF{\small,}\) такой, что две его стороны лежат на катетах, а вершина \(\displaystyle E\) – на гипотенузе треугольника. Найдите периметр квадрата.
\(\displaystyle P_{CDEF}=\) \(\displaystyle \footnotesize см{\small.}\)
По условию задачи выпоним построение.
Прямоугольный равнобедренный треугольник \(\displaystyle KLC{\small:}\)
Квадрат \(\displaystyle CDEF{\small:}\)
| 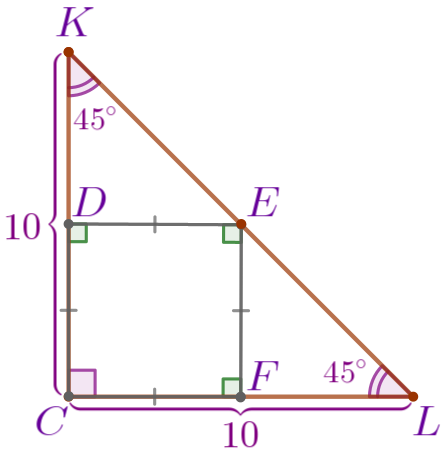 |
Требуется найти периметр квадрата \(\displaystyle CDEF{\small.}\)
| Периметр квадрата равен сумме длин всех его сторон. Пусть сторона квадрата \(\displaystyle CDEF\) равна \(\displaystyle \color{red}{x}{\small.}\) Тогда \(\displaystyle P_{CDEF}=4\cdot \color{red}{x}{\small.}\) |
Найдём \(\displaystyle \color{red}{x}{\small.}\)
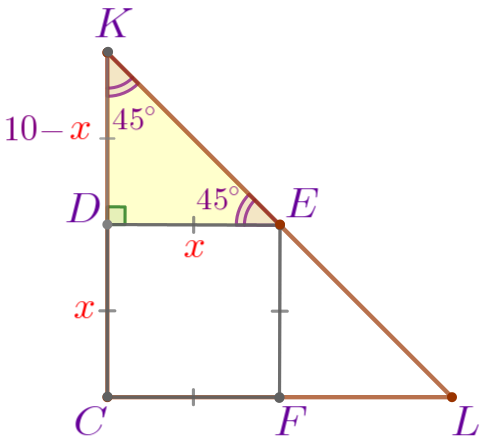
Рассмотрим прямоугольный треугольник \(\displaystyle KDE{\small.}\)
| Так как точка \(\displaystyle D\) лежит на стороне \(\displaystyle KC{\small,}\) то \(\displaystyle KD=KC-DC=10- \color{red}{x}{\small.}\) Сумма острых углов прямоугольного треугольника равна \(\displaystyle 90^{\circ}{\small.}\) Тогда \(\displaystyle \angle KED=90^{\circ}-\angle EKD=90^{\circ}-45^{\circ}=45^{\circ}{\small.}\) То есть \(\displaystyle \angle KED=\angle EKD{\small.}\) |
Значит,
\(\displaystyle \triangle KDE\) – равнобедренный.
Следовательно,
\(\displaystyle KD=DE{\small.}\)
Подставим \(\displaystyle KD=10- \color{red}{x}{\small,}\) \(\displaystyle DE=\color{red}{x}{\small:}\)
\(\displaystyle 10- \color{red}{x}=\color{red}{x}{\small;}\)
\(\displaystyle 2 \cdot \color{red}{x}=10{\small;}\)
\(\displaystyle \color{red}{x}=5{\small.}\)
Найдём периметр квадрата \(\displaystyle CDEF{\small:}\)
\(\displaystyle P_{CDEF}=4\cdot \color{red}{x}{\small;}\)
\(\displaystyle P_{CDEF}=4\cdot 5=20\, \footnotesize см{\small.}\)
Ответ: \(\displaystyle P_{CDEF}=20\, \footnotesize см{\small.}\)