Задание
Переместите точку \(\displaystyle B\) так, чтобы косинус угла \(\displaystyle AOB\) стал равен \(\displaystyle \frac{1}{3}\small.\)
В ответе напишите значение \(\displaystyle \tg\angle{AOB}\) с точностью до десятых.
\(\displaystyle \tg\angle{AOB}=\)
Решение
Определение
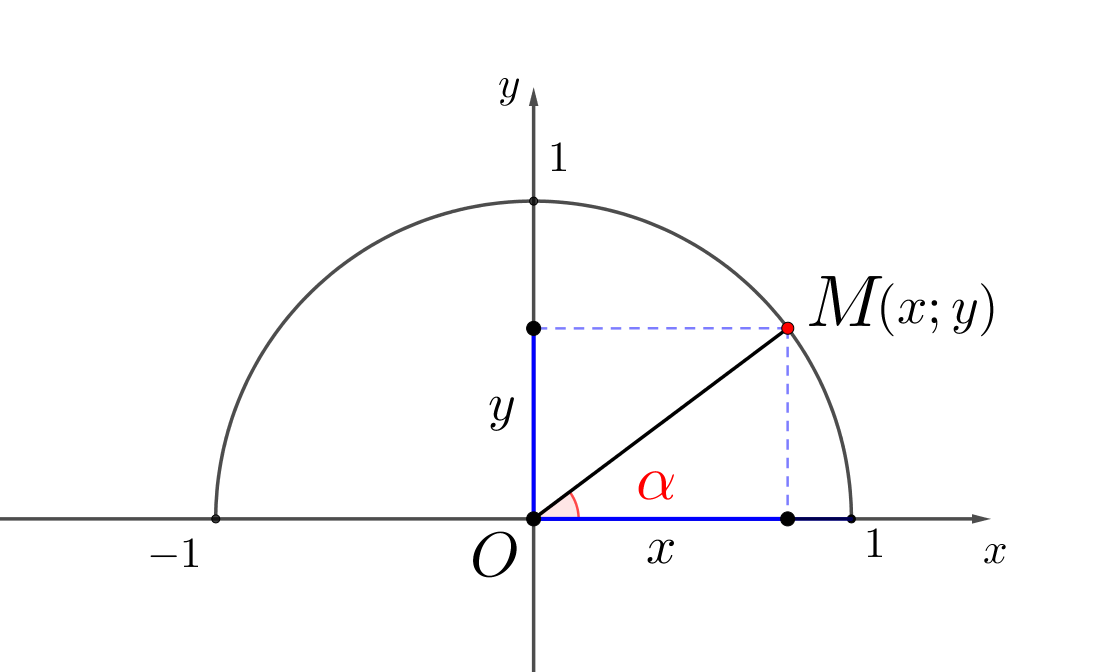
Точка \(\displaystyle M\) лежит на единичной полуокружности. Тогда для любого угла \(\displaystyle \color{red}{\alpha}\) из промежутка \(\displaystyle 0^{\circ}\leqslant\color{red}{\alpha}\leqslant180^{\circ}{\small:}\)
- косинусом угла \(\displaystyle \color{red}{\alpha}\) называется абсцисса точки \(\displaystyle M\small,\)
- синусом угла \(\displaystyle \color{red}{\alpha}\) называется ордината точки \(\displaystyle M\small.\)
Косинус угла \(\displaystyle AOB\) должен стать равным \(\displaystyle \frac{1}{3}\small.\) То есть нужно переместить точку \(\displaystyle B\) так, чтобы ее абсцисса стала равна \(\displaystyle \frac{1}{3}\small:\)
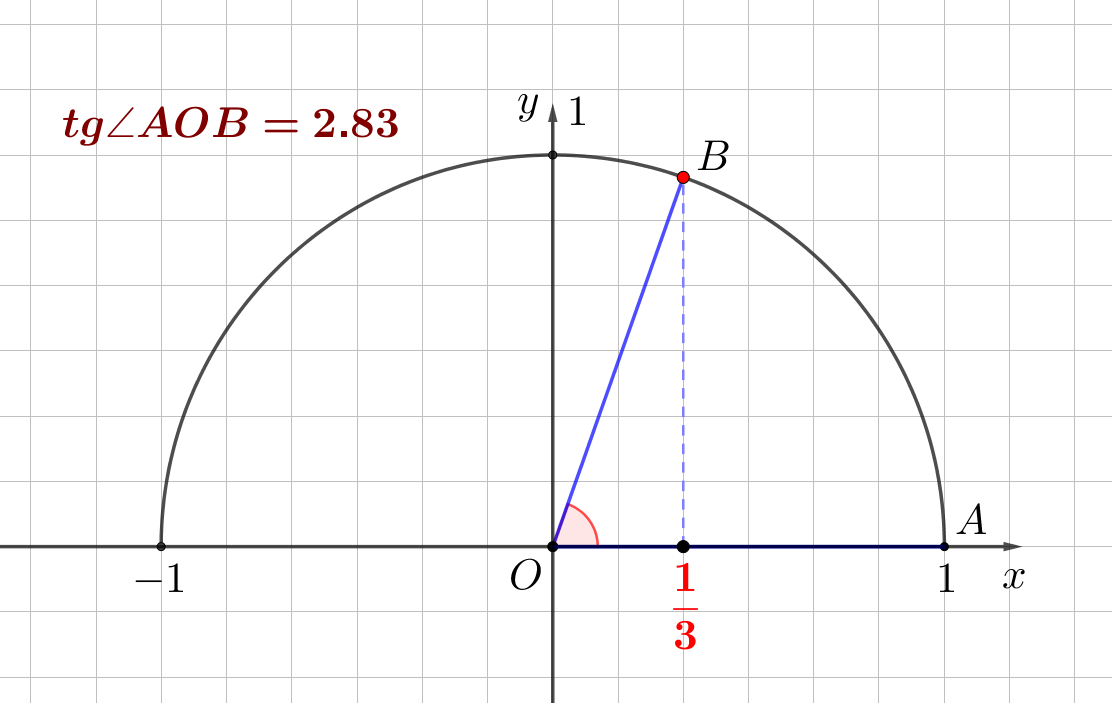
Получаем:
\(\displaystyle \tg\angle{AOB}=2{,}83\approx 2{,}8\small.\)
Ответ: \(\displaystyle 2{,}8\small.\)