На рисунке изображена единичная полуокружность, и отмечена точка\(\displaystyle N\small.\) Координаты точки \(\displaystyle N\) – \(\displaystyle (-0{,}28; 0{,}96) \small.\) Чему равны синус и косинус угла \(\displaystyle \color{red}{\alpha}\small{?}\)
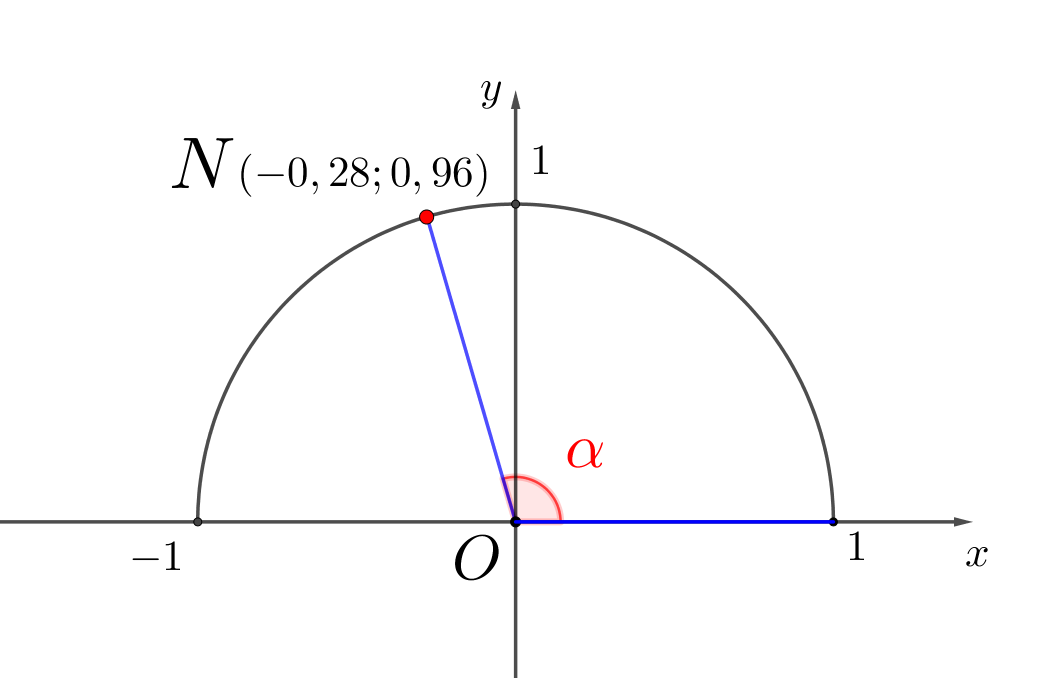
\(\displaystyle \sin\color{red}{\alpha}=\) и \(\displaystyle \cos\color{red}{\alpha}=\)
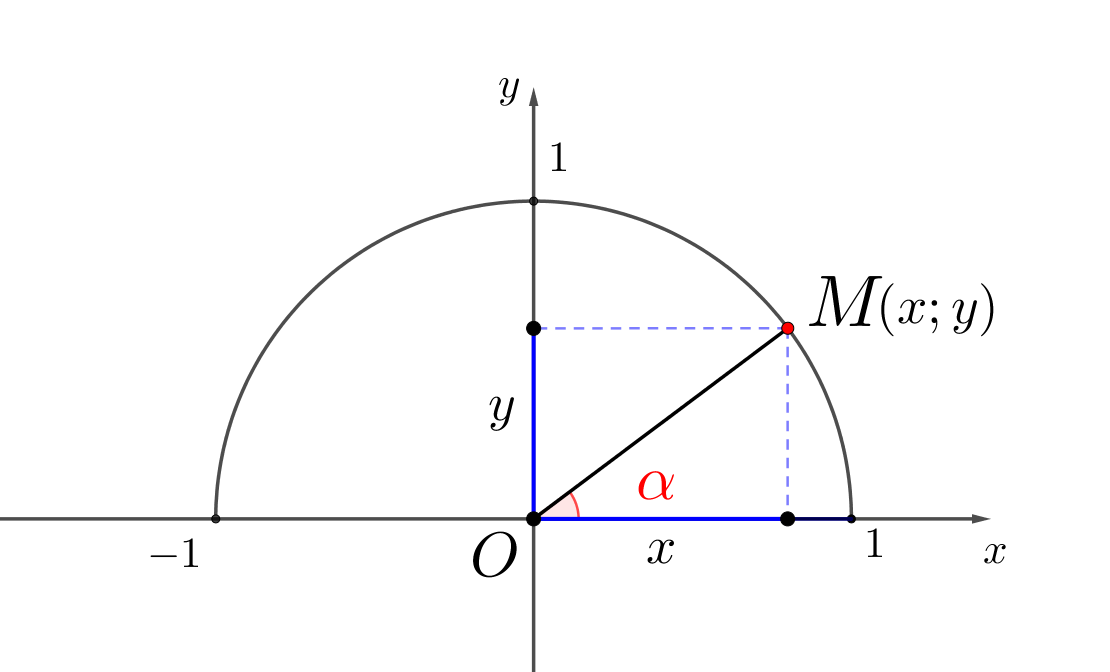
Точка \(\displaystyle M\) лежит на единичной полуокружности. Тогда для любого угла \(\displaystyle \color{red}{\alpha}\) из промежутка \(\displaystyle 0^{\circ}\leqslant\color{red}{\alpha}\leqslant180^{\circ}{\small:}\)
- косинусом угла \(\displaystyle \color{red}{\alpha}\) называется абсцисса точки \(\displaystyle M\small,\)
- синусом угла \(\displaystyle \color{red}{\alpha}\) называется ордината точки \(\displaystyle M\small.\)
На рисунке в условии задачи точка \(\displaystyle N\) имеет абсциссу \(\displaystyle -0{,}28\) и ординату \(\displaystyle 0{,}96\small.\) Тогда
\(\displaystyle \cos\color{red}{\alpha}=-0{,}28\small,\)
\(\displaystyle \sin\color{red}{\alpha}=0{,}96\small.\)