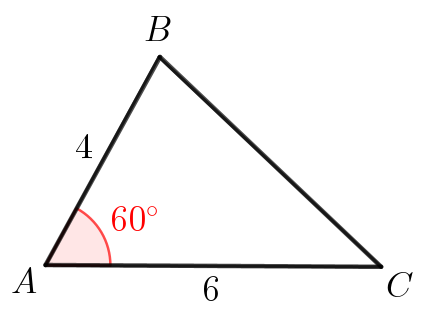
Найдите площадь треугольника \(\displaystyle ABC\small,\) если \(\displaystyle AB=4\small,\) \(\displaystyle AC=6\) и \(\displaystyle \angle BAC=60^{\circ}\small.\)
Формула площади треугольника через две стороны и угол между ними
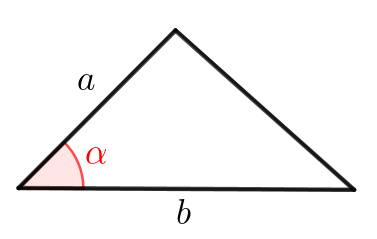
Площадь треугольника со сторонами \(\displaystyle a,\,b\) и углом \(\displaystyle \color{red}{\alpha}\) между ними равна \(\displaystyle \frac{1}{2}ab\sin\color{red}{\alpha}\small.\)
Воспользуемся формулой площади через две стороны и угол между ними: \(\displaystyle S_{ABC}=\frac{1}{2}AB\cdot AC\cdot \sin\angle BAC=\frac{1}{2}\cdot4\cdot6\cdot\sin60^{\circ}=12\sin60^{\circ}\small.\) Поскольку \(\displaystyle \sin60^{\circ}=\frac{\sqrt{3}}{2}\small,\) то \(\displaystyle S_{ABC}=12\sin60^{\circ}=12\cdot\frac{\sqrt{3}}{2}=6\sqrt{3}\small.\) |
|
Ответ: \(\displaystyle S_{ABC}=6\sqrt{3}\small.\)