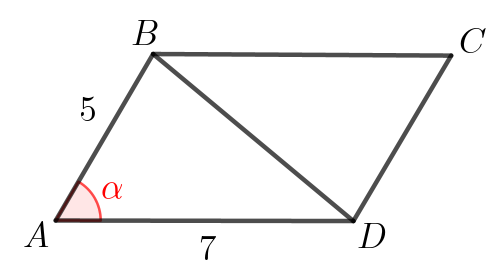
Одна сторона параллелограмма равна \(\displaystyle 5\small,\) а другая \(\displaystyle 7\small.\) При этом синус одного из углов параллелограмма равен \(\displaystyle 0{,}4\small.\) Найдите площадь этого параллелограмма.
Построим рисунок к задаче. По условию, известен синус одного из углов. Обозначим этот угол как \(\displaystyle \color{red}{\alpha}{\small .}\) Тогда \(\displaystyle \sin\color{red}{ \alpha}=0{,}4\small.\) Проведем диагональ параллелограмма. Она делит его на два равных треугольника: \(\displaystyle \bigtriangleup ABD=\bigtriangleup CBD\small.\) Площадь параллелограмма складывается из площадей этих треугольников: \(\displaystyle S_{ABCD}=S_{ABD}+S_{CBD}=2S_{ABD}\small.\) |
|
\(\displaystyle S_{ABD}=\frac{1}{2}\cdot AB\cdot AD\cdot\sin\angle BAD=\frac{1}{2}\cdot 5\cdot 7\cdot0{,}4=7\small.\)
Тогда
\(\displaystyle S_{ABCD}=2S_{ABD}=2\cdot7=14\small.\)
Ответ: \(\displaystyle S_{ABCD}=14\small.\)