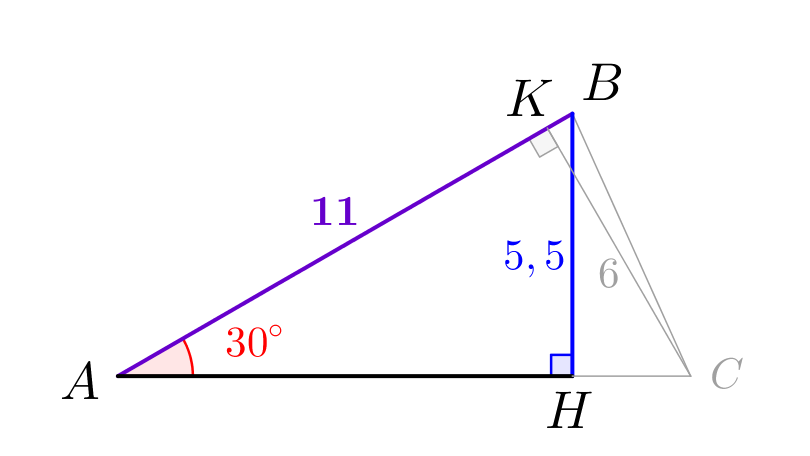
В треугольнике \(\displaystyle ABC\) угол \(\displaystyle A\) равен \(\displaystyle 30^{\circ}\small.\) Высота, проведенная из точки \(\displaystyle B\small,\) равна \(\displaystyle 5{,}5\small,\) а высота, проведенная из точки \(\displaystyle C\small,\) равна \(\displaystyle 6\small.\) Найдите площадь треугольника \(\displaystyle ABC\small.\)
Тогда, чтобы найти площадь, найдем стороны \(\displaystyle AB\small,\) \(\displaystyle AC\) и воспользуемся формулой \(\displaystyle S_{ABC}=\frac{1}{2}\cdot AB\cdot AC\cdot\sin\angle BAC\small.\) | 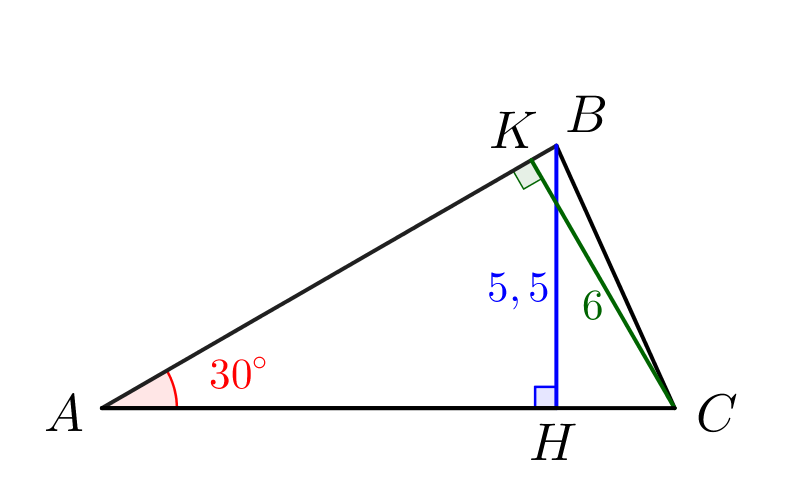 |
\(\displaystyle AC=\frac{CK}{\sin 30^{\circ}}=12\small.\)
Рассмотрим прямоугольный треугольник \(\displaystyle ACK\small.\) В этом треугольнике гипотенуза равна: \(\displaystyle AC=\frac{CK}{\sin\angle KAC}=\frac{CK}{\sin 30^{\circ}}\small.\) Поскольку \(\displaystyle CK=6\small,\) а \(\displaystyle \sin30^{\circ}=\frac{1}{2}\small,\) получаем: \(\displaystyle AC=\frac{CK}{\sin 30^{\circ}}=6:\frac{1}{2}=12\small.\) | 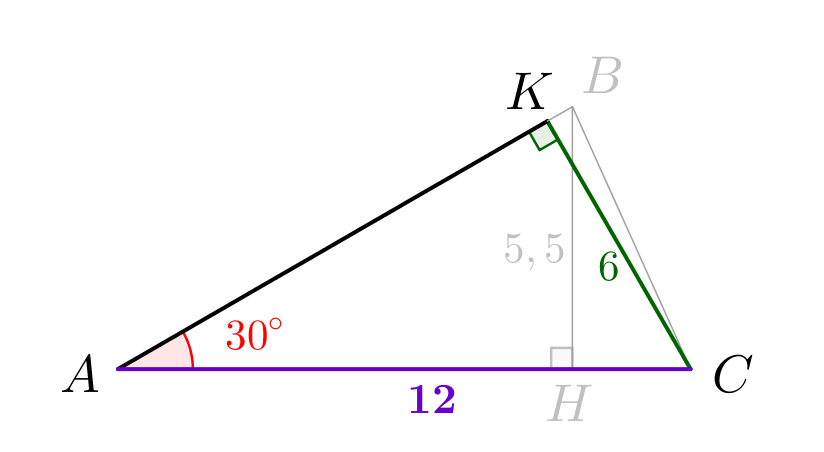 |
\(\displaystyle AB=\frac{BH}{\sin 30^{\circ}}=11\small.\)
Зная угол \(\displaystyle A\) и длину прилежащих к нему сторон, находим площадь: \(\displaystyle \begin{aligned}S_{ABC}=&\frac{1}{2}\cdot AB\cdot AC\cdot\sin\angle BAC=\\[10px]=&\frac{1}{2}\cdot11\cdot12\cdot\sin30^{\circ}=33\small.\end{aligned}\) | 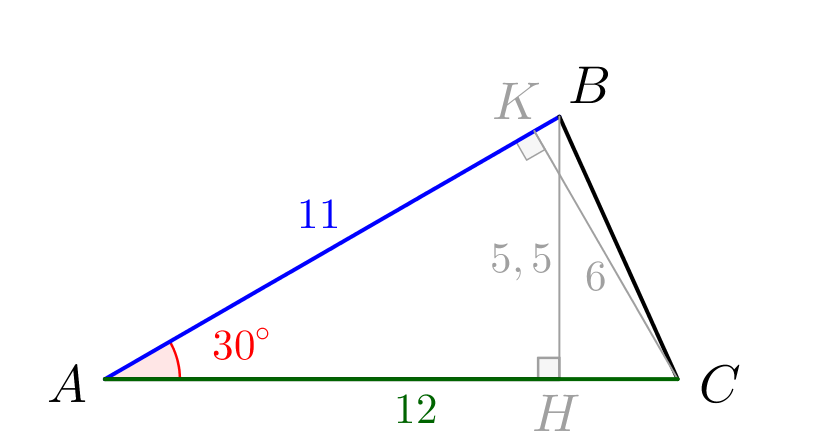 |
Ответ: \(\displaystyle S_{ABC}=33\small.\)
Отметим, что после того как мы нашли сторону \(\displaystyle AC=12\small,\) можно было сразу решить задачу, используя другую формулу нахождения площади.
Площадь равна произведению высоты и основания пополам:
\(\displaystyle S_{ABC}=\frac{AC\cdot BH}{2}=\frac{12\cdot5{,}5}{2}=33\small.\)