Задание
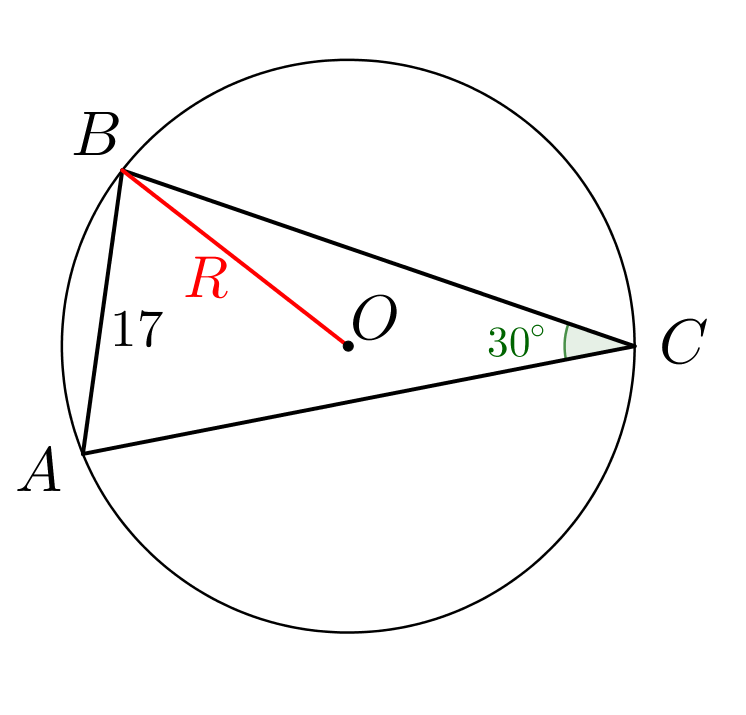
Используя теорему синусов, найдите радиус описанной окружности треугольника:
Решение
Правило
Теорема синусов
В треугольнике отношения сторон к синусам противолежащих углов одинаковы и равны удвоенному радиусу описанной окружности: \(\displaystyle \frac{\color{Purple}{a}}{\sin\color{Purple}{\alpha}}=\frac{\color{green}{b}}{\sin\color{green}{\beta}}=\frac{\color{blue}{c}}{\sin\color{blue}{\gamma}}=2\color{red}{R}{\small.}\) |  |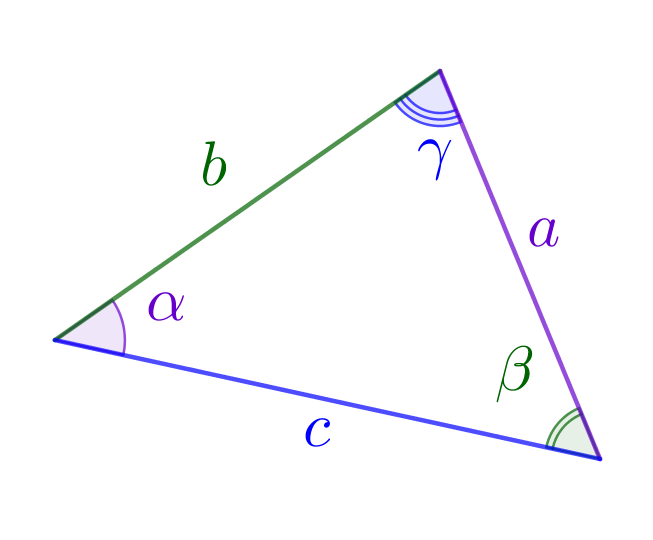
По теореме синусов для треугольника \(\displaystyle ABC\small{:}\) \(\displaystyle \frac{AB}{\sin30^\circ}=2R\small.\)
\(\displaystyle R=\frac{AB}{2\sin30^\circ}=\frac{17}{2\cdot \frac{1}{2}}=17\small.\) |  |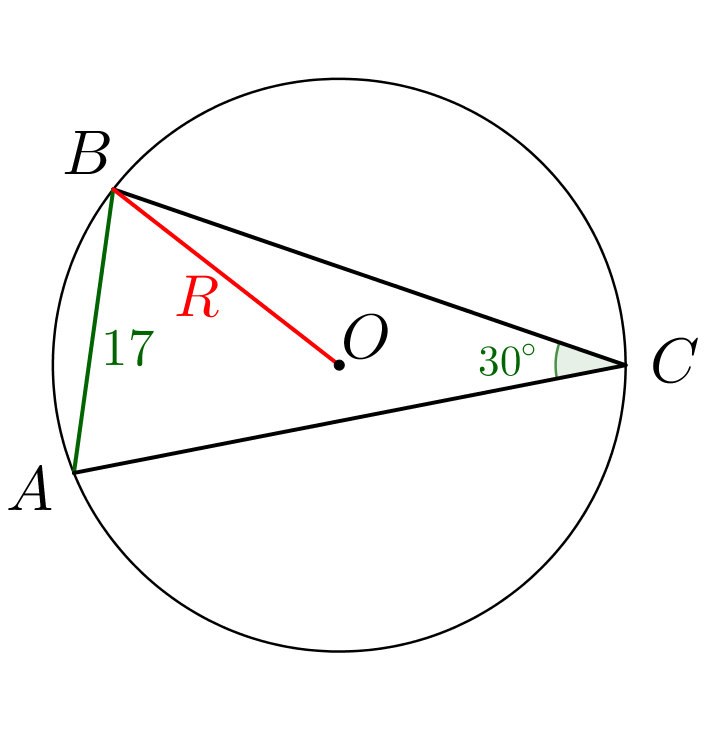
Ответ: \(\displaystyle 17\small.\)