На сторонах угла \(\displaystyle DAE\) отмечены точки \(\displaystyle B\) и \(\displaystyle C{\small .}\)
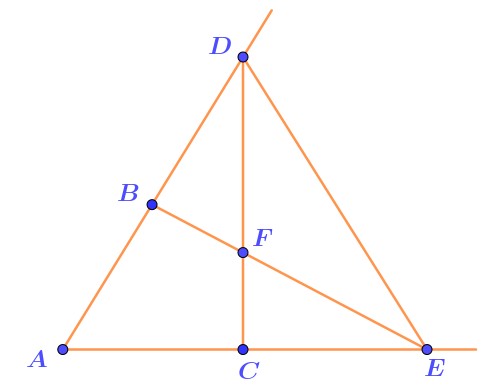
Известно, что \(\displaystyle AB=AC\) и \(\displaystyle AD=AE{\small .}\)
Какой треугольник, согласно первому признаку равенства треугольников, равен треугольнику \(\displaystyle ADC{\small ?}\)
В условии две пары равных отрезков \(\displaystyle AB=AC\) и \(\displaystyle AD=AE{\small .}\)
Заметим, что они заключают один и тот же угол \(\displaystyle DAE{\small .}\)
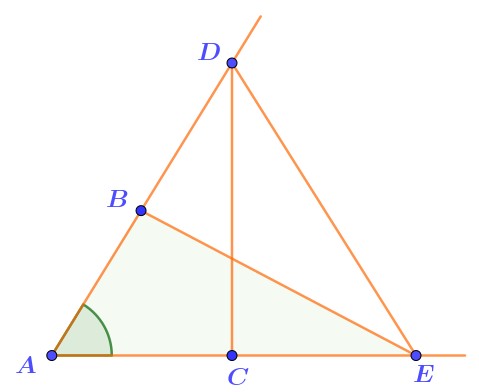
.
В этих треугольниках
\(\displaystyle \left\{\begin{array}{ll}AC=AB\\AE=AD\\{\bf\angle}A-\footnotesize {общий\,угол}\end{array}{\LARGE\Rightarrow} \quad {\bf\triangle}ADC={\bf\triangle}AEB\text{ \normalsize\it(по первому признаку)}\right.\)
Ответ: \(\displaystyle {\triangle}ADC={\triangle}AEB {\small .}\)