Задание
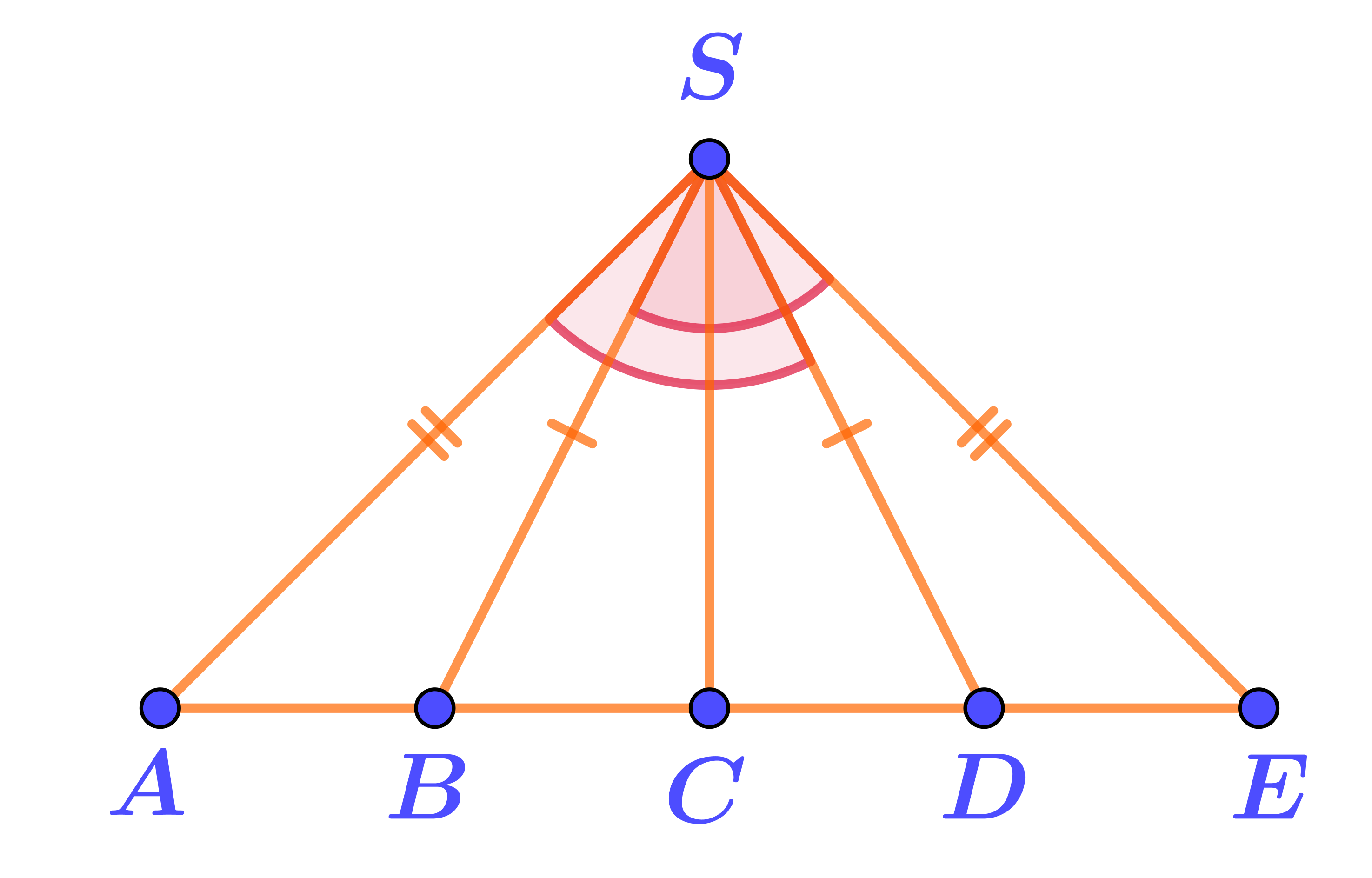
На рисунке отмечены две пары равных отрезков и равные углы \(\displaystyle ASD\) и \(\displaystyle BSE{\small .}\)
Выберите пару треугольников, равенство которых обосновано первым признаком.
Решение
На рисунке найдём два треугольника, соответствующие условиям первого признака равенства.
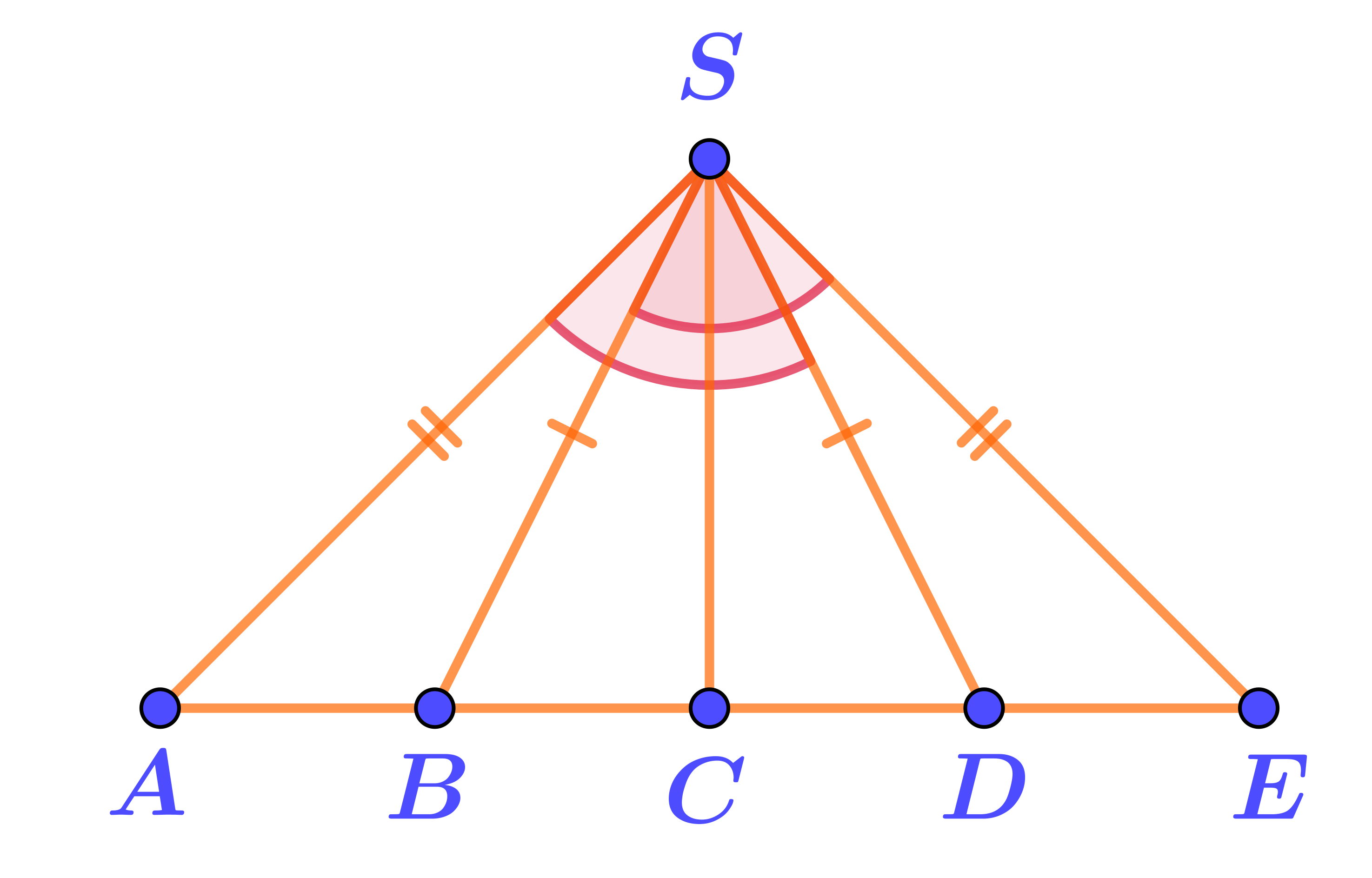
Отмечена только одна пара равных углов:
\(\displaystyle \angle ASD=\angle ESB{\small .}\)
На сторонах этих углов видим попарно равные отрезки.
Они являются сторонами треугольников \(\displaystyle ADS\) и \(\displaystyle EBS{\small .}\)
Эти треугольники равны по первому признаку:
\(\displaystyle \left\{\begin{array}{ll}AS=ES\\BS=DS\\\angle ASD=\angle ESB\end{array} {\LARGE\Rightarrow} \quad {\bf\triangle}ADS={\bf\triangle}EBS\text{ \normalsize\it(по первому признаку)}\right.\)
Ответ: \(\displaystyle {\bf\triangle}ADS={\bf\triangle}EBS{\small .}\)