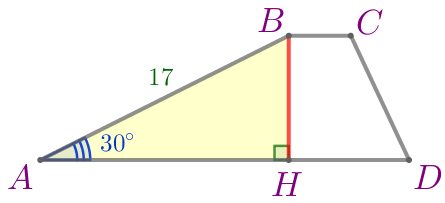
Найдите высоту трапеции \(\displaystyle ABCD{\small,}\) если боковая сторона \(\displaystyle AB=17\) и \(\displaystyle \angle ABC=150^{\circ}\small.\)
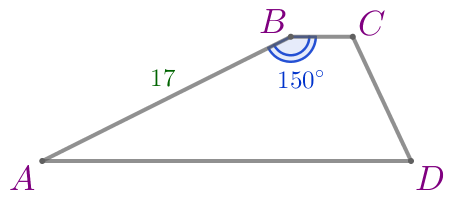 |
Требуется найти высоту данной трапеции. |
\(\displaystyle \angle A+\angle B=180^{\circ}{\small.}\)
Тогда \(\displaystyle \angle A=180^{\circ}-\angle B=180^{\circ}-150^{\circ}=30^{\circ}{\small.}\)
Проведем высоту \(\displaystyle BH \) трапеции. | 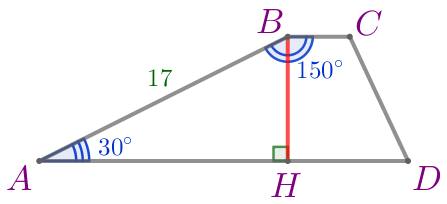 |
Рассмотрим прямоугольный треугольник \(\displaystyle ABH{\small.}\)
| В прямоугольном треугольнике катет, лежащий напротив угла \(\displaystyle 30^{\circ}{\small,}\) равен половине гипотенузы. Тогда \(\displaystyle BH=\frac{1}{2}\cdot {AB}=\frac{1}{2}\cdot 17=8{,}5{\small.}\) |
Ответ: \(\displaystyle 8{,}5 {\small.}\)