В трапеции \(\displaystyle ABCD\) угол \(\displaystyle B\) равен \(\displaystyle 150^{\circ}{\small.}\) Найдите угол \(\displaystyle A{\small.}\) Ответ запишите в градусах.
\(\displaystyle \angle A=\) \(\displaystyle ^{\circ}{\small.}\)
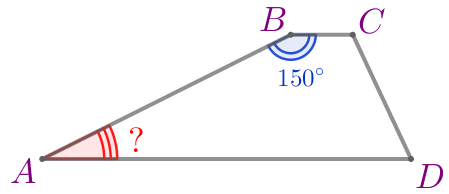 |
Требуется найти угол \(\displaystyle A{\small.}\) |
Свойство трапеции
В трапеции сумма углов, прилегающих к боковой стороне, равна \(\displaystyle 180^{\circ} {\small.}\) \(\displaystyle \color{Magenta} {\alpha} +\color{brown}{\beta}=180^{\circ}{\small,}\) \(\displaystyle \color{blue}{\gamma}+\color{green}{\varphi}=180^{\circ}{\small.}\) | 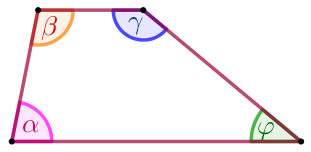 |
Согласно свойству в трапеции \(\displaystyle ABCD\)
\(\displaystyle \angle A+\angle B=180^{\circ}{\small.}\)
Тогда
\(\displaystyle \angle A=180^{\circ}-\angle B=180^{\circ}-150^{\circ}=30^{\circ}{\small.}\)
Ответ: \(\displaystyle \angle A=30^{\circ}{\small.}\)