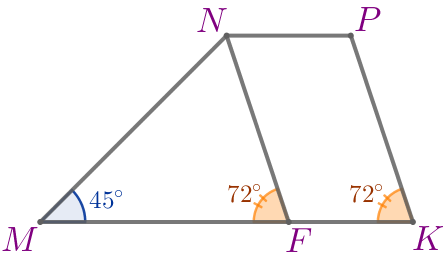
В трапеции \(\displaystyle MNPK\) большее основание \(\displaystyle MK{\small.}\) Через вершину \(\displaystyle N\) проведена прямая, параллельная стороне \(\displaystyle PK{\small,}\) до пересечения с основанием \(\displaystyle MK\) в точке \(\displaystyle F{\small,}\) \(\displaystyle \angle NMF=45^{\circ}{\small,}\) \(\displaystyle \angle MFN=72^{\circ}{\small.}\) Найдите углы трапеции.
\(\displaystyle \angle M=\) \(\displaystyle ^{\circ}{\small;}\) \(\displaystyle \angle N=\) \(\displaystyle ^{\circ}{\small;}\) \(\displaystyle \angle P=\) \(\displaystyle ^{\circ}{\small;}\) \(\displaystyle \angle K=\) \(\displaystyle ^{\circ}{\small.}\)
 |
Требуется найти углы данной трапеции. |
\(\displaystyle \angle MKP=\angle MFN=72^{\circ}{\small.}\)
Таким образом, в трапеции \(\displaystyle MNPK{\small:}\)
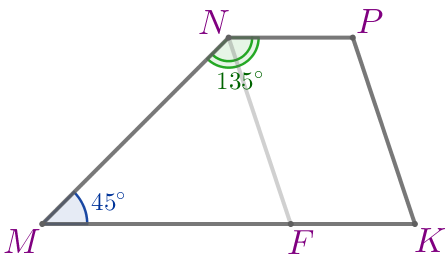
Найдём \(\displaystyle \angle N\) и \(\displaystyle \angle P{\small.}\) | 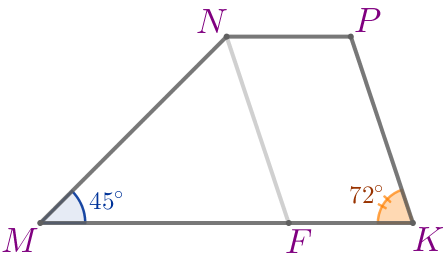 |
Свойство трапеции
В трапеции сумма углов, прилегающих к боковой стороне, равна \(\displaystyle 180^{\circ} {\small.}\) \(\displaystyle \color{Magenta} {\alpha} +\color{brown}{\beta}=180^{\circ}{\small,}\) \(\displaystyle \color{blue}{\gamma}+\color{green}{\varphi}=180^{\circ}{\small.}\) | 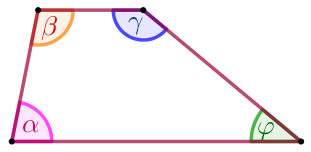 |
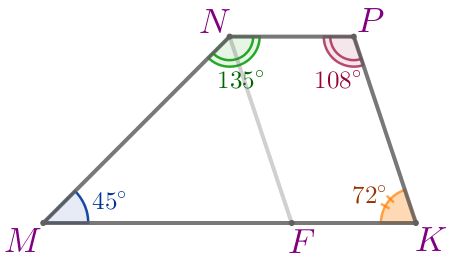
\(\displaystyle \angle N=135^{\circ}\)
\(\displaystyle \angle P=108^{\circ}\)
Ответ: \(\displaystyle \angle M=45^{\circ}{\small;}\) \(\displaystyle \angle N=135^{\circ}{\small;}\) \(\displaystyle \angle P=108^{\circ}{\small;}\) \(\displaystyle \angle K=72^{\circ}{\small.}\)